如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是 ；
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=
AD，请给出证明；
（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
如图，为测量学校围墙外直立电线杆AB的高度，小亮在操场上点C处直立高3m的竹竿CD，然后退到点E处，此时恰好看到竹竿顶端D与电线杆顶端B重合；小亮又在点C1处直立高3m的竹竿C1D1，然后退到点E1处，此时恰好看到竹竿顶端D1与电线杆顶端B重合。小亮的眼睛离地面高度EF=1.5m，量得CE=2m，EC1=6m，C1E1=3m。
（1）△FDM∽△ ▲，△F1D1N∽△ ▲；
（2）求电线杆AB的高度。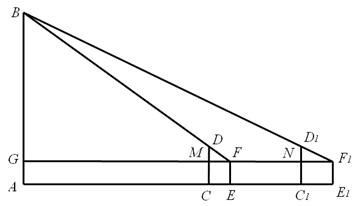
为了倡导节能低碳的生活，某公司对集体宿舍用电收费作如下规定：一间宿舍一个月用电量不超过a千瓦时，则一个月的电费为20元；若超过a千瓦时，则除了交20元外，超过部分每千瓦时要交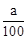
元。某宿舍3月份用电80千瓦时，交电费35元；4月份用电45千瓦时，交电费20元。
（1）求a的值；
（2）若该宿舍5月份交电费45元，那么该宿舍当月用电量为多少千瓦时？
二次函数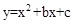
的图象经过点（4，3），（3，0）。
（1）求b、c的值；
（2）求出该二次函数图象的顶点坐标和对称轴；
（3）在所给坐标系中画出二次函数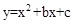的图象。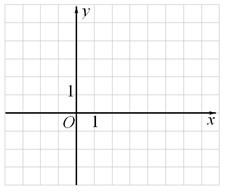
如图，C为AB的中点。四边形ACDE为平行四边形，BE与CD相交于点F。
求证：EF=BF。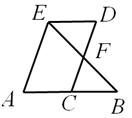
某校为了进一步开展“阳光体育”活动，计划用2000元购买乒乓球拍，用2800元购买羽毛球拍。已知一副羽毛球拍比一副乒乓球拍贵14元。该校购买的乒乓球拍与羽毛球拍的数量能相同吗？请说明理由。