如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A2处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015,到BC的距离记为h2015.若h1=1,则h2015的值为( )
A. |
B. |
C. |
D. |
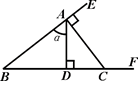
如图,CA⊥BE于A,AD⊥BF于D,下列正确的是( )
| A.α的余角只有∠B | B.α的邻补角是∠DAC |
| C.∠ACF是α的余角 | D.α与∠ACF互补 |
某商店进了一批商品,每件商品的进价为a元.若要获利15%,则每件商品的零售价应为()
| A.15%a元 | B.(1+15%)a元 | C.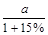 元 元 |
D.(1-15%)a元 |
如图,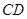 是⊙O的直径,
是⊙O的直径,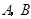 是⊙O上的两点,若
是⊙O上的两点,若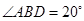 ,
,
则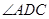 的度数为()
的度数为()
A.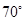 |
B.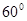 |
C.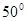 |
D.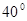 |
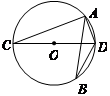
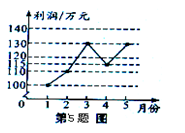
某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是()
| A.1~2月份利润的增长快于2~3月份分利润的增长 |
| B.1~4月份利润的极差与1~5月份利润的极差不同 |
| C.1~5月份利润的的众数是130万元 |
| D.1~5月份利润的中位数为120万元 |
已知四边形ABCD是平行四边形,下列结论中不正确的是()
| A.当AB=BC时,它是菱形 | B.当AC⊥BD时,它是菱形 |
| C.当∠ABC=90°时,它是矩形 | D.当AC=BD时,它是正方形 |