要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差 ,
, 哪个大;
哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
问题提出:
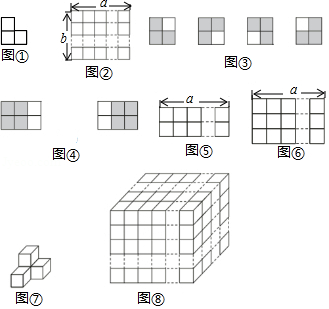
如图,图①是一张由三个边长为1的小正方形组成的“ ”形纸片,图②是一张 的方格纸 的方格纸指边长分别为 , 的矩形,被分成 个边长为1的小正方形,其中 , ,且 , 为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
问题探究:
为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:
把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图③,对于 的方格纸,要用图①盖住其中的三个小正方形,显然有4种不同的放置方法.
探究二:
把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图④,在 的方格纸中,共可以找到2个位置不同的 方格,依据探究一的结论可知,把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.
探究三:
把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑤,在 的方格纸中,共可以找到 个位置不同的 方格,依据探究一的结论可知,把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.
探究四:
把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑥,在 的方格纸中,共可以找到 个位置不同的 方格,依据探究一的结论可知,把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.
问题解决:
把图①放置在 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.
问题拓展:
如图,图⑦是一个由4个棱长为1的小立方体构成的几何体,图⑧是一个长、宽、高分别为 , , , , ,且 , , 是正整数)的长方体,被分成了 个棱长为1的小立方体.在图⑧的不同位置共可以找到 个图⑦这样的几何体.
某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量 (件 与销售单价 (元 之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 与销售单价 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于50元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 (元 最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于800元,则每天的销售量最少应为多少件?

如图,在 中,对角线 与 相交于点 ,点 , 分别为 , 的中点,延长 至 ,使 ,连接 .
(1)求证: ;
(2)当 与 满足什么数量关系时,四边形 是矩形?请说明理由.

甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工600个这种零件,甲比乙少用5天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是150元和120元,现有3000个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过7800元,那么甲至少加工了多少天?
如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 ,栈道 与景区道路 平行.在 处测得栈道一端 位于北偏西 方向,在 处测得栈道另一端 位于北偏西 方向.已知 , ,求木栈道 的长度(结果保留整数).
(参考数据: , , , , ,
