光滑水平面上静置两个小木块A和B,其质量分别为mA=150g、mB=200g,它们中间用一根轻质弹簧相连,弹簧处于原长状态。一颗水平飞行的子弹质量为m=50g,以v0=400m/s的速度在极短时间内打入木块A并镶嵌在其中,求系统运动过程中弹簧的最大弹性势能。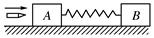
2008年9月25日,载人航天宇宙飞船“神舟七号”发射成功,且中国人成功实现了太空行走,并顺利返回地面. 设飞船在太空环绕时轨道高度为h,地球半径为R,地面重力加速度为g,飞船绕地球遨游太空的总时间为t,则“神舟七号”飞船绕地球运转多少圈?(用给定字母表示)
如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受的拉力达到F=18N时就会被拉断;当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断;若此时小球距水平面的高度h=5m,重力加速度g取10m/s2,求小球落地处与细线恰被拉断时的位置间的距离?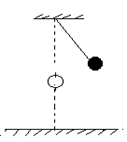
一静止的 核经 衰变成为 核,释放出的总动能为4.27 。问此衰变后 核的动能为多少 (保留1位有效数字)?
一玻璃三棱镜,其截面为等腰三角形,顶角 为锐角,折射率为 。现在横截面内有一光线从其左侧面上半部射入棱镜。不考虑棱镜内部的反射。若保持入射线在过入射点的法线的下方一侧(如图),且要求入射角为任何值的光线都会从棱镜的右侧面射出,则顶角 可在什么范围内取值?

如图,一气缸水平固定在静止的小车上,一质量为
、面积为
的活塞将一定量的气体封闭在气缸内,平衡时活塞与气缸底相距
。现让小车以一较小的水平恒定加速度向右运动,稳定时发现活塞相对于气缸移动了距离
。已知大气压强为
,不计气缸和活塞间的摩擦,且小车运动时,大气对活塞的压强仍可视为
,整个过程中温度保持不变。求小车的加速度的大小。