在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
完成下列解答过程:
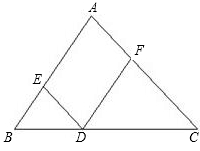
证明:(1)∵∠A=_______,(已知)
∴AC∥ED.(_______)
(2)∵∠EDF=_______,(已知)
∴AC∥ED.(_______)
(3)∵∠A+∠DFA=180°(已知)
∴_______∥_______.(_______)
如图,已知a∥b,∠3+∠2=180°,b与c平行吗?说明理由.
先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使CE=CA,连接AE;
(2)求证:CD∥AE.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,将△ADC沿AC边所在的直线折叠,使点D落在点E处,得四边形ABCE.
求证:EC∥AB.
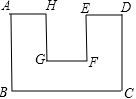
如图所示,在一个凹型图形中,下列说法都正确吗?如果不正确,请加以更正.
(1)∠H与∠A是同旁内角,∠H与∠G是内错角;
(2)与∠D互为同旁内角的角只有∠C;
(3)图中没有同位角.