光明文具厂工人的工作时间:每月26天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资920元,按月结算.该厂生产A,B两种型号零件,工人每生产一件A种型号零件,可得报酬0.85元,每生产一件B种型号零件,可得报酬1.5元,下表记录的是工人小王的工作情况:
| 生产A种型号零件/件 |
生产B种型号零件/件 |
总时间/分 |
| 2 |
2 |
70 |
| 6 |
4 |
170 |
根据上表提供的信息,请回答如下问题:
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目限制,那么小王该月的工资数目最多为多少?
如图,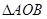 的顶点A、B在二次函数
的顶点A、B在二次函数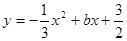 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在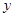 轴和
轴和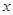 轴上,
轴上,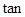 ∠ABO=
∠ABO=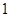 .
.
(1)求此二次函数的解析式;
|
(2)过点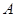 作
作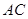 ∥
∥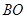 交上述函数图像于点
交上述函数图像于点 ,
,
 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.
的坐标.
(本题满分12 分)
分)
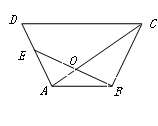
如图,梯形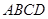 中,
中,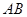 ∥
∥ ,
,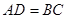 ,点
,点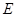 在边
在边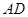 上,
上, 与
与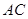 相交于点
相交于点 ,且
,且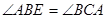 .
.
求证:(1)
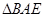 ∽
∽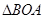 ;
; (2)
 .
.
小楠家附近的公路上通行车辆限速为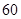 千米/小时.小楠家住在距离公路
千米/小时.小楠家住在距离公路 米的居民楼(
米的居民楼( 如图8中的P点处),在他家前有一道路指示牌
如图8中的P点处),在他家前有一道路指示牌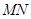 正好挡住公路上的
正好挡住公路上的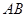 段(即点
段(即点 和点
和点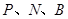 分别在一直
分别在一直 线上),已知
线上),已知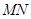 ∥
∥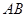 ,
, 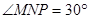 ,
, ,小楠看见一辆卡车通过
,小楠看见一辆卡车通过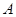 处,
处, 秒后他在
秒后他在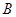 处再次看见这辆卡车,他认定这辆卡车一定超速,你同意小楠的结论吗?请说明理由. (参考数据:
处再次看见这辆卡车,他认定这辆卡车一定超速,你同意小楠的结论吗?请说明理由. (参考数据: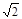 ≈1.41,
≈1.41,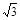 ≈1.73)
≈1.73)
如图,在 中,点
中,点 在边
在边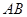 上,点
上,点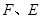 在边
在边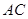 上,且
上,且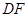 ∥
∥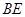 ,
, .
.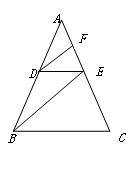
(1)求证:
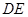 ∥
∥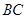 ;
;(2)如果
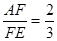 ,
,
 ,求
,求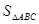 的值.
的值.
如图,□ 中,
中, ∥
∥ ,
, ∥
∥ ,点
,点 是
是 的中点,
的中点, 和
和 相交于点
相交于点 .
.
(1)求
 的值;
的值; (2)如果
(2)如果 ,
, ,请用
,请用 、
、 表示
表示