如图，已知抛物线
（
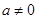）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．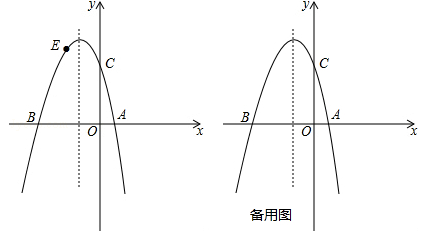
（1）求此抛物线的解析式；
（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；
（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．
一架飞机在两城之间飞行，风速为24千米/小时．顺风飞行需要2小时50分，逆风飞行需要3小时，求无风时飞机的航速和两城之间的航程．
解下列方程：
（1）2(x＋1)=3(x―2)；
（2）
．
粮库3天发生粮食进出库的吨数如下（“＋”表示进库，“－”表示出库）：
＋26，－32，－15，＋34，－38，－20．
（1）经过这3天，库里的粮食是增多还是减少了；
（2）经过这3天，仓库管理员结算发现库里还存480吨粮，那么3天前库里存粮多少吨？
（3）如果进出的装御费都是每吨5元，那么这3天要付多少装卸费？
计算：
（1）－12＋(―18)―(―7)―15；
（2）
设a=
，b=
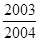，c=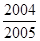
，比较a，b，c的大小．（提示：用整数1分别减去a，b，c）