如图1，A1B1和A2B2是水面上相邻的两条赛道（看成两条互相平行的线段）．甲是一名游泳运动健将，乙是一名游泳爱好者，甲在赛道A1B1上从A1处出发，到达B1后，以同样的速度返回A1处，然后重复上述过程；乙在赛道A2B2上以2m/s的速度从B2处出发，到达A2后以相同的速度回到B2处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两人同时出发，设离开池边B1B2的距离为y（m），运动时间为t（s），甲游动时，y（m）与t（s）的函数图象如图2所示．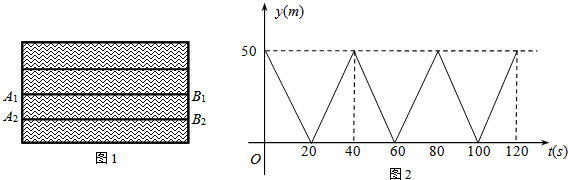
（1）赛道的长度是 m，甲的速度是 m/s；
（2）经过多少秒时，甲、乙两人第二次相遇？
（3）若从甲、乙两人同时开始出发到2分钟为止，甲、乙共相遇了 次．2分钟时，乙距池边B1B2的距离为多少米．
+
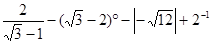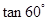
如图，P是⊙O外一点，OP垂直于弦AB于点C，交
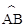于点D，连结OA、OB、AP、BP。根据以上条件，写出三个正确结论（OA=OB除外）：(6分)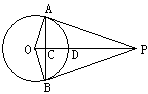
①②___；③。
已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分
∠BCD，DF∥AB，BF的延长线交DC于点E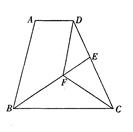
△BFC≌△DFC
AD=DE．
现有足够的1元、2元的人民币，需要把面值为10元人民币换成零钱，请你设计几种兑换方案．
若等式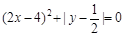
中的x、y满足方程组
求2m2－n＋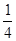
mn的值．
根据题意列出方程组：
(1)某班共有学生42人，男生比女生人数的2倍少6人，问男、女生各有多少人?
(2)某玩具厂要生产一批玩具，若每天生产35个，则差10个才能完成任务；若每天生产40个，则可超额生产20个．求预定期限是多少天?计划生产多少个玩具?
拓展、探究、思考