如图所示,在△ABC中,∠ABC=∠ACB.
(1)尺规作图:过顶点A作△ABC的角平分线AD;(不写作法,保留作图痕迹)
(2)在AD上任取一点E,连接BE、CE.求证:△ABE≌△ACE.
如图,将一块直角三角形纸板的直角顶点放在C(1, )处,两直角边分别与
)处,两直角边分别与 轴平行,纸板的另两个顶点
轴平行,纸板的另两个顶点 恰好是直线
恰好是直线 与双曲线
与双曲线 的交点.
的交点.
(1)求 和
和 的值;
的值;
(2)设双曲线 在
在 之间的部分为
之间的部分为 ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点 在
在 上滑动,两直角边始终与坐标轴平行,且与线段
上滑动,两直角边始终与坐标轴平行,且与线段 交于
交于 两点,请探究是否存在点
两点,请探究是否存在点 使得
使得 ,写出你的探究过程和结论.
,写出你的探究过程和结论.
已知一次函数y=2x-k与反比例函数 的图像相交于A和B两点.,如果有一个交点A的横坐标为3,
的图像相交于A和B两点.,如果有一个交点A的横坐标为3,
(1)求k的值;
(2)求A、B两点的坐标;
(3)根据图象写出一次函数的值大于反比例函数的值的 的取值范围
的取值范围
(4)求△AOB的面积;
水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
在一个不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为 .
.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
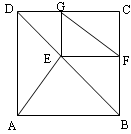
如图,E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F、G.求证:AE=FG.