如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.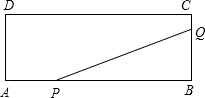
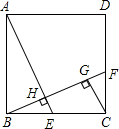
如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3) .
.
周日里,我和爸爸、妈妈在家都想使用电脑上网,可是家里只有一台电脑啊,怎么办?为了公平起见我设计了下面的两种游戏规则,确定谁使用电脑上网.
(1)任意投掷两枚质地均匀的硬币,若两枚正面都朝上,则爸爸使用电脑;若两枚反面都朝上,妈妈使用电脑;若一枚正面朝上一枚反面朝上,则我使用电脑.
(2)任意投掷两枚骰子,若点数之和被3整除,则爸爸使用电脑;若点数之和被3除余数为1,则妈妈使用电脑;若点数之和被3除余数为2,则我使用电脑.
请你来评判,这两种游戏规则哪种公平,并说明理由噢!
某学校后勤人员到一家文具店给九年级的同学购买考试用文具包,文具店规定一次购买400个以上,可享受8折优惠.若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,就可享受8折优惠,同样只需付款1936元.请问该学校九年级学生有多少人?
解不等式组: 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.