英国特技演员史蒂夫·特鲁加里亚曾飞车挑战世界最大环形车道.如图所示,环形车道竖直放置,直径达12 m,若汽车在车道上以12 m/s恒定的速率运动,演员与汽车的总质量为1 000 kg,重力加速度g取10 m/s2,则( )

| A.汽车通过最低点时,演员处于超重状态 |
| B.汽车通过最高点时对环形车道的压力为1.4×104 N |
| C.若要挑战成功,汽车不可能以低于12 m/s的恒定速率运动 |
| D.汽车在环形车道上的角速度为1 rad/s |
如图所示,物体A放在粗糙板上随板一起在竖直平面内沿逆时针方向做匀速圆周运动,且板始终保持水平,位置Ⅰ、Ⅱ在同一水平高度上,则( )
| A.物体在位置Ⅰ、Ⅱ时受到的弹力都大于重力 |
| B.物体在位置Ⅰ、Ⅱ时受到的弹力都小于重力 |
| C.物体在位置Ⅰ时受到的弹力小于重力,位置Ⅱ时受到的弹力都大于重力 |
| D.物体在位置Ⅰ时受到的弹力大于重力,位置Ⅱ时受到的弹力都小于重力 |
如图所示,P点与 N点等高,Q点有一光滑钉子,Q点与E点等高,O是摆的悬点,O、 N、Q、M在同一竖直线上.Q为MN的中点.将质量为m的摆球拉到与竖直方向成60°的P点后无初速释放.当球摆到最低点时悬线被钉子挡住,球沿以Q为中心的圆弧继续运动,下列对小球第一次过M点后的描述和最终状态的描述中正确的是( )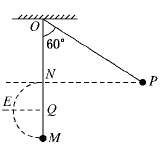
| A.在过M点后小球向左摆到 N点后自由下落 |
| B.在过M点后小球将在 NM之间做自由下落 |
| C.在过M点的瞬间,绳对小球的拉力为小球重力的5倍 |
| D.小球最终将绕Q点来回摆动 |
如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间恰好无作用力,则( )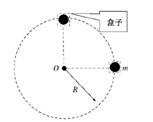
A.该盒子做匀速圆周运动的周期一定小于2π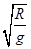 |
B.该盒子做匀速圆周运动的周期一定等于2π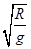 |
| C.盒子在最低点时盒子与小球之间的作用力大小可能小于2mg |
| D.盒子在最低点时盒子与小球之间的作用力大小可能小于2mg |
汽车甲和汽车乙质量相等,以相等的速率沿同一水平弯道做匀速圆周运动,甲车在乙车的外侧.两车沿半径方向受到的摩擦力分别为f甲和f乙.以下说法正确的是( )
| A.f甲小于f乙 |
| B.f甲等于f乙 |
| C.f甲大于f乙 |
| D.f甲和f乙大小均与汽车速率无关 |
甲、乙两名溜冰运动员,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示.已知M甲="80" kg,M乙="40" kg,两人相距0.9m,弹簧秤的示数为96 N,下列判断中正确的是( )
| A.两人的线速度相同,约为40 m/s |
| B.两人的角速度相同,为2 rad/s |
| C.两人的运动半径相同,都是0.45 m |
| D.两人的运动半径不同,甲为0.3 m,乙为0.6 m |