已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
列方程(组)解应用题:
国家的“家电下乡”政策激活了农民购买能力,提高了农民的生活水平。“家电下乡”的补贴标准是:农户每购买一件家电,国家将按每件家电售价的13%补贴给农户.李大叔购买了一台彩电和一台洗衣机,从乡政府领到了390元补贴款.若彩电的售价比洗衣机的售价高1000元,求彩电和洗衣机的售价各是多少元.
当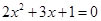 时 ,求
时 ,求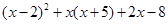 的值.
的值.
如图,已知线段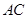 与
与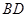 相交于点
相交于点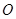 ,联结
,联结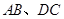 ,
,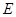 为
为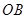 的中点,
的中点,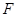 为
为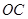 的中点,联结
的中点,联结 .若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.
.若∠A=∠D,∠OEF=∠OFE,求证:AB=DC.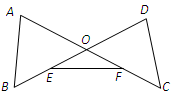
(本小题满分12分)阅读下列内容,设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三边长间的关系来判断这个三角形的形状:
①若 ,则该三角形是直角三角形;②若
,则该三角形是直角三角形;②若 ,则该三角形是钝角三角形;③
,则该三角形是钝角三角形;③ ,则该三角形是锐角三角形.
,则该三角形是锐角三角形.
例如一个三角形的三边长分别是4,5,6,则最长边是6,由于 ,故由上面③可知该三角形是锐角三角形,请解答以下问题:
,故由上面③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是三角形;
(2)若一个三角形的三条边长分别是3,4,x且这个三角形是直角三角形,则x的值为;
(3)若一个三角形的三条边长分别是 ,
, ,
, 请判断这个三角形的形状,并写出的判断过程.
请判断这个三角形的形状,并写出的判断过程.
(本小题满分10分)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)