某中学为了了解本校八年级女生“一分钟跳绳”项目基础情况,从八年级随机抽取部分女生进行该项目测试,并将测试所得的数据,绘制成如图所示的部分频数分布直方图(从左到右依次分为第一小组,第二小组…第六小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题:
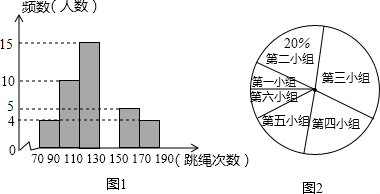
(1)补全频数分布直方图.
(2)计算在扇形统计图中第一小组对应的扇形的圆心角度数.
(3)这次测试成绩的中位数落在第 小组.
(4)若测试八年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校八年级女生共有400人,请估算该校八年级女生“一分钟跳绳”成绩为优秀的人数.
已知:如图, 内接于⊙
内接于⊙ ,点
,点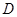 在
在 的延长线上,
的延长线上, .
.
(1)求证: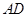 是⊙
是⊙ 的切线;(2)若
的切线;(2)若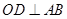 ,
,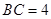 ,求
,求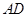 的长.
的长.
如图,点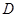 、
、 分别为
分别为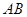 、
、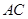 边上两点,且
边上两点,且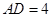 ,
, ,
,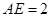 ,
, .(1)试说明:
.(1)试说明: ∽
∽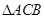 ;(2)若
;(2)若 ,求
,求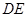 的长.
的长.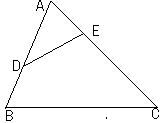
(本题满分7分)果农李明种植的草莓计划以每千克 元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,价格连续两次下调后,以每千克
元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,价格连续两次下调后,以每千克 元的单价对外批发销售.
元的单价对外批发销售.
(1)求李明平均每次下调的百分率;
(2)小刘准备到李明处购买 吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:方案一:在原下调后价格的基础上,再次以相同的百分率降价;方案二:不打折,每吨优惠现金
吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:方案一:在原下调后价格的基础上,再次以相同的百分率降价;方案二:不打折,每吨优惠现金 元.试问小刘选择哪种方案更优惠,请说明理由.
元.试问小刘选择哪种方案更优惠,请说明理由.
如图,在由边长为1的小正方形组成的网格图中有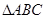 ,建立平面直角坐标系后,点
,建立平面直角坐标系后,点 的坐标是
的坐标是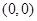 .
.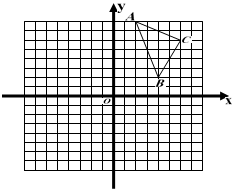
(1)以 为位似中心,作
为位似中心,作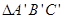 ∽
∽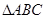 ,相似比为
,相似比为 ,且保证
,且保证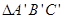 在第三象限;
在第三象限;
(2)点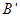 的坐标为(,);
的坐标为(,);
(3)若线段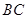 上有一点
上有一点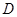 ,它的坐标为
,它的坐标为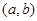 ,那么它的对应点
,那么它的对应点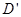 的坐标为(,).
的坐标为(,).
已知关于 的方程
的方程 .
.
(1)试说明:无论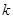 取什么实数值,方程总有实数根;
取什么实数值,方程总有实数根;
(2)若等腰 的一边长
的一边长 为1,另两边长
为1,另两边长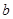 、
、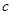 恰好是这个方程的两个实数根,求
恰好是这个方程的两个实数根,求 的周长.
的周长.