某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.

(1)请你根据图中的数据,填写下表;
| 姓名 |
平均数 |
众数 |
方差 |
| 王亮 |
|
7 |
|
| 李刚 |
7 |
|
2.8 |
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,游戏规则如下:
(1)请用树状图或列表法表示一个回合所有可能出现的结果。
(2)求一个合能确定两人先下棋的概率。
如图,在△ABC中,∠A=300, ,BC=
,BC= ,求AB的长。
,求AB的长。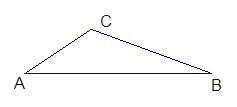
如图,抛物线与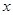 轴交于
轴交于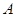 (
(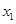 ,0)、
,0)、 (
( ,0)两点,且
,0)两点,且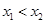 ,与
,与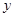 轴交于点
轴交于点 ,其中
,其中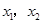 是方程
是方程 的两个根。
的两个根。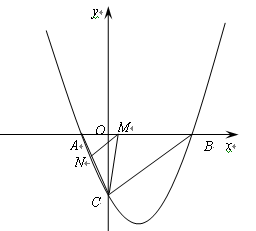
(1)求抛物线的解析式;
(2)点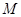 是线段
是线段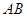 上的一个动点,过点
上的一个动点,过点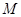 作
作 ∥
∥ ,交
,交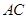 于点
于点 ,连接
,连接 ,当
,当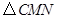 的面积最大时,求点
的面积最大时,求点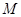 的坐标;
的坐标;
(3)点 在(1)中抛物线上,点
在(1)中抛物线上,点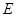 为抛物线上一动点,在
为抛物线上一动点,在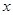 轴上是否存在点
轴上是否存在点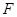 ,使以
,使以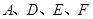 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点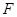 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
如图,已知Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连结BD。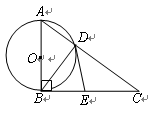
(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连结DE,求证:ED与⊙O相切。
如图,为举办毕业联欢会,小颖设计了一个游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘上的指针所指字母都相同时,他就获得一次指定一位到会者为大家表演节目的机会。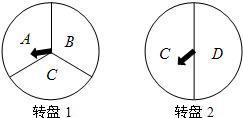
(1)利用树形图或列表的方法表示出游戏可能出现的所有结果。
(2)若小明参加一次游戏,则他能获得这种指定机会的概率是多少?