如图，二次函数y=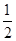
x2+bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点坐标是（8，6）．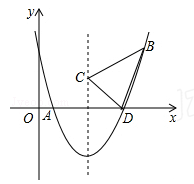
（1）求二次函数的解析式；
（2）求函数图象的顶点坐标及D点的坐标；
（3）二次函数的对称轴上是否存在一点C，使得△CBD的周长最小？若C点存在，求出C点的坐标；若C点不存在，请说明理由．
已知：如图，△ABC中，∠C=90°，AC=6，BC=8，D、E分别是AB、BC上的点，且BD=4，BE="5" 求证：DE⊥AB 
已知：如图，在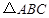
中，D是AC上一点，联结BD，且∠ABD =∠ACB.
求证：△ABD∽△ACB；
若AD=5，AB= 7，求AC的长.
在直角坐标系xoy中，已知点P是反比例函数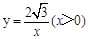
图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．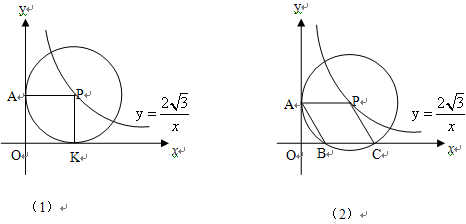
（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与x轴相交，设交点为B、C．当四边形ABCP是菱形时，求出点A、B、C的坐标．
如图，直线y=3x+3交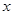
轴于A点，交
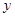轴于B点，过A、B两点的抛物线交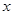轴于另一点C（3，0）．（1）求抛物线的解析式；（2）求抛物线的对称轴和顶点坐标． 
我县开展小组合作学习，为了解学生课堂发言情况，随机抽取某校九年级部分学生，对他们每天在课堂上发言的次数进行调查和统计，统计表如下，并绘制了两幅不完整的统计图．已经知A、B两组发言人数直方图高度比为1:5．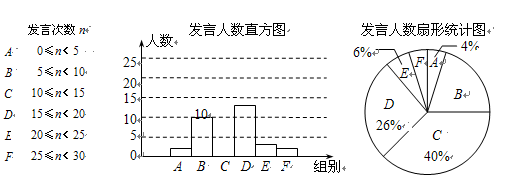
请结合图中相关的数据回答下列问题：
（1）A组的人数是多少？本次调查的样本容量是多少？
（2）求出C组的人数并补全直方图．
（3）该校九年级共有250人，请估计全年级每天在课堂上发言次数不少于15次的人数．