如图，在平面直角坐标系中，抛物线y=a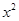
+bx﹣3（a≠0）与x轴交于点A（﹣2，0）、B（4，0）两点，与y轴交于点C．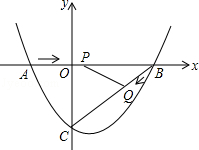
（1）求抛物线的解析式；
（2）点P从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，当△PBQ存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？
（3）当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使S△CBK：S△PBQ=5：2，求K点坐标．
已知：如图，在□ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC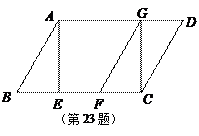
求证：BE＝DG
若∠B＝60°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？说明你的理由．
某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：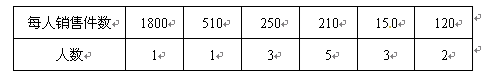
求这15位营销人员该月销售量的平均数、中位数、众数
假设销售部负责人把每个营销人员的月销售量定为320件，你认为是否合理，为什么？如果不合理，请你制定一个较为合理的销售定额，并说明理由.
用甲乙两种饮料按照x：y(重量比)混合配制成一种新饮料，原来两种饮料成本是：甲每500
克5元，乙每500克4元。现甲成本上升10%，乙下降10%，而新饮料成本恰好保持不变，
则x：y=。
| A．4：5 | B．3：4 | C．2：3 | D．1：2 。 |
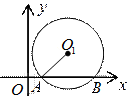
已知：如图，⊙O1与坐标轴交于A（1，0）、B（5，0）两点，点O1的纵坐标为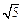
．求⊙O1的半径．