根据阳泉市教育局3月份通知，从2016年中考起，九年级学生信息技术考试成绩统计入中考总分，我县某中学为了提高八年级学生学习信息技术的积极性，组织了“信息技术技能竞赛”活动，八年级甲、乙两班根据初赛成绩，各选出5名选手参加复赛，这些选手的复赛成绩（满分为100分）如图所示：
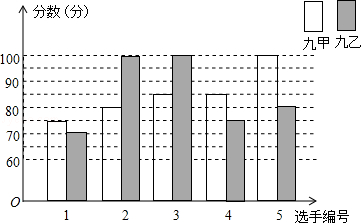
（1）根据统计图填写下表：
班级 平均数 众数 方差
甲班 85 85
乙班 160
（2）根据上表可知，两个班选手成绩较稳定的是 ；
（3）选手小明说：“这次竞赛我得了80分，在我们班选手中成绩排名属下游！（后两名）”观察统计图，求出两班选手成绩的中位数，说明小明是哪个班的学生？
（4）学校要给其中一个班发集体优胜奖，你认为发给哪个班合适？请综合考评，说明理由．
先化简：（x﹣
）÷
，其中的x选一个适当的数代入求值．
如图，二次函数
的图象与x轴相交于点A（﹣3，0）、B（1，0），与y轴相交于点C，点G是二次函数图象的顶点，直线GC交x轴于点H（3，0），AD平行GC交y轴于点D．
（1）求该二次函数的表达式；
（2）求证：四边形ACHD是正方形；
（3）如图2，点M（t，p）是该二次函数图象上的动点，并且点M在第二象限内，过点M的直线
交二次函数的图象于另一点N．
①若四边形ADCM的面积为S，请求出S关于t的函数表达式，并写出t的取值范围；
②若△CMN的面积等于
，请求出此时①中S的值．
如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点．
（1）求证：△ADP≌△ECP；
（2）若BP=n•PK，试求出n的值；
（3）作BM丄AE于点M，作KN丄AE于点N，连结MO、NO，如图2所示，请证明△MON是等腰三角形，并直接写出∠MON的度数．
如图，某渔船在小岛O南偏东75°方向的B处遇险，在小岛O南偏西45°方向A处巡航的中国渔政船接到求救信号后立刻前往救援，此时，中国渔政船与小岛O相距8海里，渔船在中国渔政船的正东方向上．
（1）求∠BAO与∠ABO的度数（直接写出答案）；
（2）若中国渔政船以每小时28海里的速度沿AB方向赶往B处救援，能否在1小时内赶到？请说明理由．（参考数据：tan75°≈3.73，tan15°≈0.27，
≈1.41，
≈2.45）
为了治理大气污染，我国中部某市抽取了该市2014年中120天的空气质量指数，绘制了如下不完整的统计图表：
请根据图表中提供的信息，解答下面的问题：
（1）空气质量指数统计表中的a=，m=；
（2）请把空气质量指数条形统计图补充完整：
（3）若绘制“空气质量指数扇形统计图”，级别为“优”所对应扇形的圆心角是度；
（4）估计该市2014年（365天）中空气质量指数大于100的天数约有天．