已知 与
与 之间的几组数据如下表:
之间的几组数据如下表:
 |
1 |
2 |
3 |
4 |
5 |
6 |
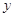 |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为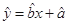 .若某同学根据上表中前两组数据
.若某同学根据上表中前两组数据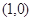 和
和 求得的直线方程为
求得的直线方程为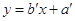 ,则以下结论正确的是()。xx。k.Com]
,则以下结论正确的是()。xx。k.Com]
A.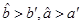 B.
B.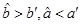 C.
C.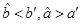 D.
D.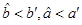
学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为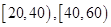 ,
, ,若低于60分的人数是15人,则该班的学生人数是()
,若低于60分的人数是15人,则该班的学生人数是() 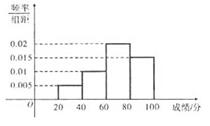
| A.45 | B.50 | C.55 | D.60 |
某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=()
| A.9 | B.10 | C.12 | D.13 |
集合A={2,3},B={1,2,3},从A,B中各取任意一个数,则这两数之和等于4的概率是()
A.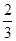 |
B.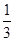 |
C.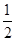 |
D. |
执行如图所示的程序框图,若输入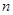 的值为3,则输出
的值为3,则输出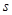 的值是()
的值是()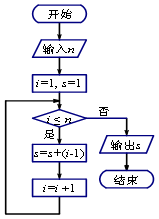
| A.1 | B.2 | C.4 | D.7 |