如图,四面体 的三条棱
的三条棱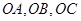 两两垂直,
两两垂直, ,
,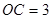 ,
,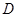 为四面体
为四面体 外一点.给出下列命题.
外一点.给出下列命题.

①不存在点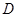 ,使四面体
,使四面体 有三个面是直角三角形
有三个面是直角三角形
②不存在点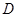 ,使四面体
,使四面体 是正三棱锥
是正三棱锥
③存在点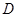 ,使
,使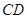 与
与 垂直并且相等
垂直并且相等
④存在无数个点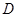 ,使点
,使点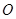 在四面体
在四面体 的外接球面上
的外接球面上
其中真命题的序号是 ( )
| A.①② | B.②③ | C.③ | D.③④ |
已知数列{an}的前n项和Sn=n2-6n,数列{|an|}的前n项和Tn,则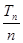 的最小值是()
的最小值是()
A.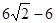 |
B. |
C.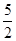 |
D.3 |
若函数f(x)=lnx-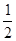 ax2-2x存在单调递减区间,则实数a的取值范围是()
ax2-2x存在单调递减区间,则实数a的取值范围是()
A.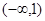 |
B. |
C.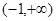 |
D. |
已知函数f(x)是定义在R上的奇函数,且是以2为周期的周期函数.若当x∈[0,1)时,f(x)=2x-1,则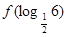 的值为()
的值为()
A.-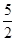 |
B.-5 | C.-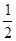 |
D.-6 |
函数f(x)=2cos2x- sin2x(x∈R)的最小正周期和最小值分别为 ()
sin2x(x∈R)的最小正周期和最小值分别为 ()
| A.2π,3 | B.2π,-1 | C.π,3 | D.π,-1 |
已知圆C的方程为x2+y2+2x-2y+1=0,当圆心C到直线kx+y+4=0的距离最大时,k的值为()
A. |
B. |
C. |
D. |