如图,点A(2,2)在双曲线y1= (x>0)上,点C在双曲线y2=-
(x>0)上,点C在双曲线y2=-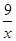 (x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
(1)求k的值;
(2)求证:△BCE≌△ABF;
(3)求直线BD的解析式.
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
某市一楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人现在准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?
如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.