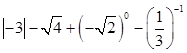为了预防H7N9禽流感，某学校对教室采用药熏消毒法进行消毒．已知，药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例，药物燃烧后，y与x成反比例（如图所示）．现测得药物4分钟燃毕，此室内空气中每立方米的含药量为8毫克，请你根据题中所提供的信息，解答下列问题：
（1）求出药物燃烧时与药物燃烧后y与x的函数关系式，并写出相应的自变量的取值范围 。
（2）研究表明，当空气中每立方米的含药量不低于2毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？
如图，在△ABC中，CD⊥AB于D，AC＝20，BC＝15，DC＝12。
(1)求AB的长。
（2）判断△ABC的形状，并说明理由。
先化简,再求值: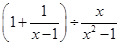 
，选一个你喜欢的数字代入求值。
解分式方程：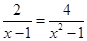 
计算：(1)
