为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:

设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
已知y=x2+px+q,当x=1时,y的值为2;当x=-2时,y的值为2。求x=-3时y的值。
解不等式组,并把解集表示在数轴上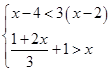
解方程组 (每题6分,共12分)
(1) (2)
(2)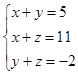
已知抛物线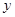 =
=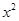 +
+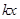 +
+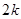 -4.
-4.
(1)当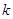 =2时,求出此抛物线的顶点坐标;
=2时,求出此抛物线的顶点坐标;
(2)求证:无论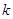 为什么实数,抛物线都与
为什么实数,抛物线都与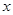 轴有交点,且经过
轴有交点,且经过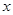 轴上的一定点;
轴上的一定点;
(3)已知抛物线与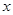 轴交于A(
轴交于A(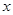 1,0)、B(
1,0)、B(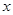 2,0)两点(A在B的左边),|
2,0)两点(A在B的左边),|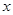 1|<|
1|<|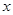 2|,与
2|,与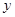 轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.
轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.
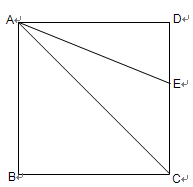
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,点P、Q分别是边AD和AE上的动点(两动点都不与端点重合).
(1)PQ+DQ的最小值是 ;
(2)说出PQ+DQ取得最小值时,点P、点Q的位置,并在图8中画出;
(3)请对(2)中你所给的结论进行证明.