如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.
(1)当t=0.5时,求△BPQ的面积;
(2)设⊙O的面积为y,求y与t的函数解析式,并直接写出y的值最小时t的值;
(3)若⊙O与Rt△ABC的一条边相切,求t的值.
(广安)“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.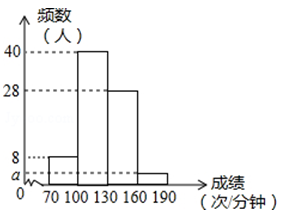
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.
(广元)图1是某中学九年级一班全体学生对三种水果喜欢人数的频数分布统计图.根据图中信息回答下列问题: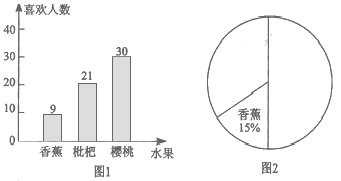
(1)九年级一班总人数有多少人?
(2)喜欢哪种水果人数的频数最低?并求出该频率;
(3)请根据频数分布统计图(图1)的数据,补全扇形统计图(图2);
(4)某水果摊位上正好只摆放有这三种水果出售,王阿姨去购买时,随机购买其中两种水果,恰好买到樱桃和枇杷的概率是多少?用村状图或列表说明.
(绵阳)阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
(1)前10株西红柿秧上小西红柿个数的平均数是 ,中位数是 ,众数是 ;
(2)若对这20个数按组距为8进行分组,请补全频数分布表及频数分布直方图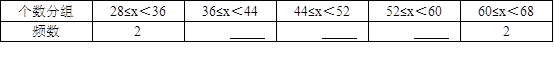
(3)通过频数分布直方图试分析此大棚中西红柿的长势.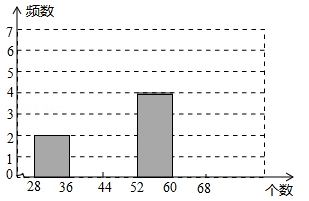
(眉山)(本小题满分9分)某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.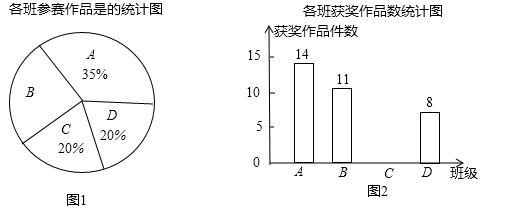
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
(泸州)小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).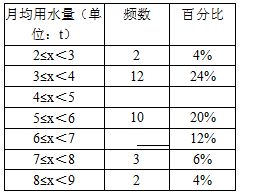
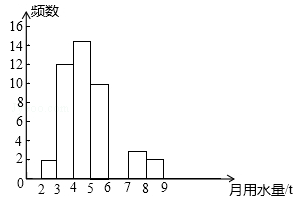
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.