(1)从宏观现象中总结出来的经典物理学规律不一定都能适用于微观体系。但是在某些问题中利用经典物理学规律也能得到与实际比较相符合的结论。
例如，玻尔建立的氢原子模型，仍然把电子的运动看做经典力学描述下的轨道运动。他认为，氢原子中的电子在库仑力的作用下，绕原子核做匀速圆周运动。已知电子质量为m，电荷为e，静电力常量为k，氢原子处于基态时电子的轨道半径为r1。
(1)氢原予处于基态时，电子绕原子核运动，可等效为环形电流，求此等效电流值。
(2)在微观领域，动量守恒定律和能量守恒定律依然适用。
a．己知光在真空中的速度为c，氢原子在不同能级之间跃迁时，跃迁前后可认为质量不变，均为m。设氢原子处于基态时的能量为E1(E1<O)，当原子处于第一激发态时的能量为E1/4，求原子从第一激发态跃迁到基态时，放出光子的能量和氢原子的反冲速度。
b．在轻核聚变的核反应中，两个氘核(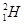
)以相同的动能Eo=0.35MeV做对心碰撞，假设该反应中释放的核能全部转化为氦核(
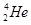)和中子（
）的动能。已知氘核的质量mD=2.0141u，中子的质量mn=1.0087u，氦核的质量MHe=3.0160u，其中1u相当于931MeV。在上述轻核聚变的核反应中生成的氦核和中子的动能各是多少MeV（结果保留1位有效数字）?
如图所示，两个完全相同的球，重力大小均为G ，两球与水平地面间的动摩擦因数都为μ，且假设最大静摩擦力等于滑动摩擦力，一根轻绳两端固结在两个球上，在绳的中点施加一个竖直向上的拉力，当绳被拉直后，两段绳间的夹角为α.问当F至少为多大时，两球将会发生滑动？
一辆汽车性能的优劣，其油耗标准非常重要，而影响汽车油耗标准最主要的因素是其在行进中所受到的空气阻力．人们发现汽车在高速行驶中所受到的空气阻力Ff(也称风阻)主要与两个因素有关．一是汽车正面投影面积S；二是汽车行驶速度
.
某研究人员在汽车风洞实验室中通过模拟实验得到下列所列数据：
（1）请写出由上述数据得出的汽车风阻Ff与汽车正面投影面积S及汽车行驶的速度的关系式(可以用k表示比例系数)．
(2) 请由上述数据求出比例系数k的大小和单位．
如图所示，质量为20kg的方形物体置于水平面上，它与水平面之间的动摩擦因数为μ，两等长轻弹簧OA、OB一端分别连接于物体上相距为24cm的A、B两点，另一端共同连结于O点。当两轻弹簧刚好处于自由状态时，它们构成了一个1060的张角。现用一垂直于AB连线的水平力F向右拉O点，当把两弹簧之间的张角拉成740时，物体恰好能在水平面上匀速前进，此时两弹簧还等长。求动摩擦因数μ的大小。(已知弹簧的劲度系数为k =1000N/m sin370=0.6 g=10m/s2 )
如图所示， \倾角为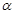
的斜面体（斜面光滑且足够长）固定在水平地面上，斜面顶端与劲度系数为
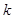、自然长度为
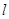的轻质弹簧相连，弹簧的另一端连接着质量为
的物块。压缩弹簧使其长度为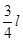
时将物块由静止开始释放（物快做简谐运动），且物块在以后的运动中，斜面体始终处于静止状态。重力加速度为
。
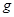（1）求物块处于平衡位置时弹簧的长度；
（2）物块做简谐运动的振幅是多少；
（3）选物块的平衡位置为坐标原点，沿斜面向下为正方向建立坐标轴，用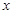
表示物块相对于平衡位置的位移，证明物块做简谐运动；（已知做简谐运动的物体所受的恢复力满足 F=—kx）
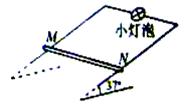
如图所示，足够长平行金属导轨倾斜放置，倾角为37°，宽度为0.5m，电阻忽略不计，其上端接一小灯泡，电阻为1Ω。一导体棒MN垂直于导轨放置，质量为0.2kg，接入电路的电阻为1Ω，两端与导轨接触良好，与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场，磁感应强度为0.8T。将导体棒MN由静止释放，运动一段时间后，小灯泡稳定发光，求此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为是多少？（重力加速度g取10m/s2，sin37°=0.6）