已知向量a=(1,2),b=(x+1,-x),且a⊥b,则x=( )
| A.2 | B. |
C.1 | D.0 |
下列命题中,错误的是 ( )
| A.一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| B.平行于同一平面的两个不同平面平行 |
C.如果平面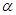 不垂直平面 不垂直平面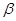 ,那么平面 ,那么平面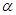 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面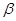 |
D.若直线 不平行平面 不平行平面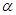 ,则在平面 ,则在平面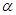 内不存在与 内不存在与 平行的直线 平行的直线 |
函数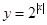 的定义域为
的定义域为 ,值域为
,值域为 ,
,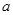 变动时,方程
变动时,方程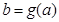 表示的图形可以是()
表示的图形可以是()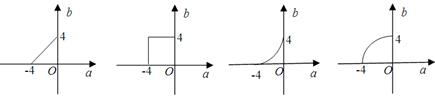
A. B. C.D.
已知△ABC为等边三角形, ,设点P,Q满足
,设点P,Q满足 ,
, ,
, ,若
,若 ,则
,则 ( )
( )
A.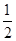 |
B. |
C.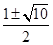 |
D. |
已知 ,不等式
,不等式 的解集为
的解集为 ,且
,且 ,则
,则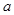 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. 或 或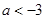 |
D. 或 或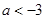 |
下列命题中,错误的是 ( )
| A.一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| B.平行于同一平面的两个不同平面平行 |
C.如果平面 不垂直平面 不垂直平面 ,那么平面 ,那么平面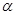 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面 |
D.若直线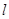 不平行平面 不平行平面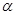 ,则在平面 ,则在平面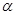 内不存在与 内不存在与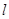 平行的直线 平行的直线 |