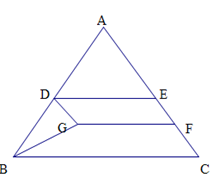
已知:Rt△ABC中,∠C=90°,∠CAB的平分线与外角∠CBE的平分线相交于点D.
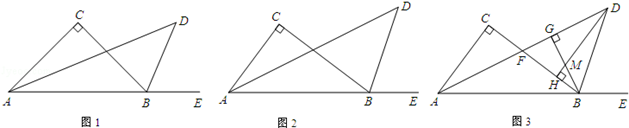
(1)如图1,若CA=CB,则∠D= 度;
(2)如图2,若CA≠CB,求∠D的度数;
(3)如图3,在(2)的条件下,AD与BC相交于点F,过B作BG⊥DF,过D作DH⊥BF,垂足分别为G,H,BG,DH相交于点M.若FG=2,DG=4,求BH的长.
为迎接“五一”国际劳动节,某公司机床车间举行“车工技能竞赛”活动,竞赛规则:先车好240个零件的选手获胜.小李为了这次比赛刻苦训练、积极准备,在比赛中,小李每小时比原来多车10个零件,结果比原来提前2小时完成任务,荣获第一名.问小李比赛中每小时车多少个零件?
如图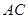 和
和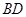 相交于点
相交于点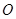 ,
,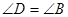 ,
,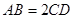 .
.
(1)如果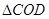 的周长是9,求
的周长是9,求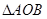 的周长;
的周长;
(2)连结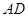 ,如果
,如果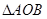 的面积是16,求
的面积是16,求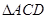 的面积.
的面积.
如图,在 中,点
中,点 ,点
,点 在
在 轴正半轴上,且
轴正半轴上,且 .
.
(1)求点 的坐标;
的坐标;
(2)将 绕原点
绕原点 顺时针旋转
顺时针旋转 ,点
,点 落在
落在 轴正半轴的点
轴正半轴的点 处,抛物线
处,抛物线 经过点
经过点 两点,求此抛物线的解析式及对称轴.
两点,求此抛物线的解析式及对称轴.
化简: .
.
如图,在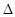
 中,
中, ,
,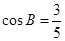 ,点
,点 在
在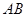 边上(点
边上(点 与点
与点 、
、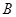 不重合),
不重合), ∥
∥ 交
交 边与点
边与点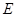 ,点
,点 在线段
在线段 上,且
上,且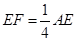 ,以
,以 、
、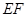 为邻边作平行四边形
为邻边作平行四边形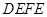 联结
联结 .
.
(1)当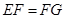 时,求
时,求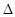
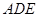 的面积;
的面积;
(2)设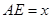 ,
,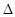
 的面积为
的面积为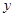 ,求
,求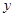 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)如果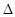
 是以
是以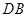 为腰的等腰三角形,求
为腰的等腰三角形,求 的值.
的值.