如图1，在一次航海模型船训练中，A1B1和A2B2是水面上相邻的两条赛道（看成两条互相平行的线段）．甲船在赛道A1B1上从A1处出发，到达B1后，以同样的速度返回A1处，然后重复上述过程；乙船在赛道A2B2上以2m/s的速度从B2处出发，到达A2后以相同的速度回到B2处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两船同时出发，设离开池边B1B2的距离为y（m），运动时间为t（s），甲船运动时，y（m）与t（s）的函数图象如图2所示．
（1）赛道的长度是 m，甲船的速度是 m/s；
（2）分别求出甲船在0≤t≤30和30＜t≤60时，y关于t的函数关系式；
（3）求出乙船由B2到达A2的时间，并在图2中画出乙船在3 分钟内的函数图象；
（4）请你根据（3）中所画的图象直接判断，若从甲、乙两船同时开始出发到3分钟为止，甲、乙共相遇了几次？
（本题6分） 解不等式：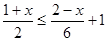
，并把解表示在数轴上．
（本题12分）如图，在△ABC中，已知AB＝AC，∠BAC＝90o，BC＝6cm，，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒2厘米的速度运动，动点E也同时从点C开始在直线CM上（向上或向下）以每秒1厘米的速度运动，连结AD、AE，设运动时间为t秒．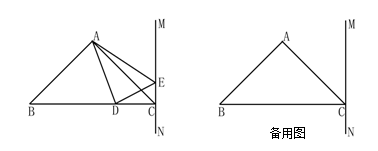
（1）求AB的长；
（2）当t为多少时，△ABD的面积为6cm2？
（3）当t为多少时，△ABD≌△ACE，并简要说明理由（可在备用图中画出具体图形）．
（本题12分）如图，是一个运算流程．
（1）分别计算：当x＝150时，输出值为，当x＝27时，输出值为；
（2）若需要经过两次运算，才能运算出y，求x的取值范围；
（3）请给出一个x的值，使之无论运算多少次都不能输出，并请说明理由．
（本题10分）如图甲，已知：在△ABC中，∠BAC＝90º，AB＝AC，直线m经过点A，BD⊥直线m， CE⊥直线m，垂足分别为点D、E，设BD＝m，CE＝n．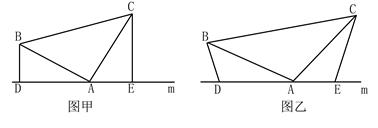
（1）求DE的长（用含m，n的代数式表示）；
（2）如图乙，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝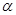
（0º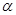＜＜180º），设BD＝m，CE＝n．问DE的长如何表示？并请证明你的结论
（本题10分）如图，在△ABC中，AB＝AC，AD是BC边上的高，AM是△ABC外角∠CAE的平分线．
（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）
（2）设DN与AM交于点F，判断△ADF的形状，并证明你的结论．