如图,在 中, , , .动点 从 点出发,沿 方向以每秒5个单位长度的速度向 点匀速运动,动点 从 点同时出发,以相同的速度沿 方向向 点匀速运动,当点 运动到 点时, 、 两点同时停止运动,以 为边作正 、 、 按逆时针排序),以 为边在 上方作正 ,设点 运动时间为 秒.
(1)求 的值;
(2)当 与 的面积满足 时,求 的值;
(3)当 为何值时, 的某个顶点 点除外)落在 的边上.

如图,在 中, ,以 为直径的 分别与 、 交于点 、 ,过点 作 于点 .
(1)若 的半径为3, ,求阴影部分的面积;
(2)求证: 是 的切线;
(3)求证: .

如图,在平面直角坐标系中, 点的坐标为 , 轴于点 , ,反比例函数 的图象的一支分别交 、 于点 、 .延长 交反比例函数的图象的另一支于点 .已知点 的纵坐标为 .
(1)求反比例函数的解析式;
(2)求直线 的解析式;
(3)求 .

已知 中, .
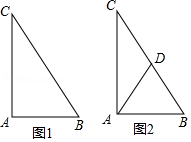
(1)请在图1中作出 边上的中线(保留作图痕迹,不写作法);
(2)如图2,设 边上的中线为 ,求证: .
攀枝花市出租车的收费标准是:起步价5元(即行驶距离不超过2千米都需付5元车费),超过2千米以后,每增加1千米,加收1.8元(不足1千米按1千米计).某同学从家乘出租车到学校,付了车费24.8元.求该同学的家到学校的距离在什么范围?