.如图甲所示，竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成，AB和BCD相切于B点，CD连线是圆轨道竖直方向的直径（C、D为圆轨道的最低点和最高点），已知∠BOC =30˚。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下，用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F，并得到如图乙所示的压力F与高度H的关系图象，取g=10m/s2。求：
（1）滑块的质量和圆轨道的半径；
（2）是否存在某个H值，使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点。若存在，请求出H值；若不存在，请说明理由。
如图所示，在水平地面上固定一倾角θ=37°、表面光滑的斜面，物体A以
的初速度沿斜面上滑，同时在物体A的正上方，物体B以某一初速度
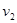水平抛出。如果当A上滑到最高点时恰好被B物体击中（A、B均可看作质点， sin37°=0.6，cos37°=0.8，g取10m/s2）。求：
（1）物体A上滑到最高点所用的时间t；
（2）物体B抛出时的初速度。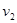
（3）物体A、B间初始位置的高度差h。
如图，传送带与地面倾角θ=30°，AB长度为
，传送带以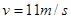
的速率逆时针转动.在传送带上端A无初速度地放上一个质量为
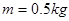的物体，它与传送带之间的动摩擦因数为
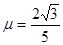,取
，则：
（1）从物体开始运动至物体刚与传送带达到共同速度这一过程中,传送带的摩擦力对物体做了多少功?
（2）物体从与传送带达到共同速度的瞬间至滑到B端的过程中，传送带的摩擦力对物体又做了多少功?
如图所示，轻杆长为3L， 在杆的A、B两端分别固定质量均为
的球A和球B，杆上距球A为L处的点O装在光滑水平转动轴上，杆和球在竖直面内转动，已知球A运动到最高点时，球A对杆恰好无作用力。求： 
（1）球A在最高点时的角速度大小；
（2）球A在最高点时，杆对水平轴的作用力的大小和方向。
如图所示，在距地面高为H=45m处，有一小球A以初速度
水平抛出，与此同时，在A的正下方有一物块B也以相同的初速度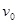
同方向滑出，B与地面间的动摩擦因数为
。A、B均可视为质点，空气阻力不计，重力加速度取
，求：
（1）A球落地时间及其抛出的水平距离。
（2）A球落地时，A、B相距多远。
在某星球上，宇航员用弹簧秤称得质量为m的砝码重力为F，乘宇宙飞船在靠近该星球表面空间飞行，测得其环绕周期为T。根据上述数据，试求该星球的质量。