如图所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长。圆环从A处由静止释放后,经过B处速度最大,到达C处(AC = h)时速度减为零。若在此时给圆环一个竖直向上的速度v,它恰好能回到A点。弹簧始终在弹性限度内,重力加速度为g,则圆环
| A.下滑过程中,加速度一直增大 |
B.下滑过程中,克服摩擦力做的功为 |
C.在C处弹簧的弹性势能为  |
| D.上下两次经过B点的速度大小相等 |
一质量m、电荷量+q的圆环,可在水平放置的足够长的粗糙细杆上滑动.细杆处于磁感应强度为B的匀强磁场中.现给圆环向右初速度v0,以后的运动过程中圆环运动的速度图象可能是()

下列有关带电粒子运动的说法中正确的是(不考虑重力)()
| A.沿着电场线方向飞入匀强电场,动能、速度都变化 |
| B.沿着磁感线方向飞入匀强磁场,动能、速度都不变 |
| C.垂直于磁感线方向飞入匀强磁场,动能、速度都变化 |
| D.垂直于磁感线方向飞入匀强磁场,速度不变,动能改变 |
如图所示,A、B两闭合圆形线圈用同样导线且均绕成10匝,半径RA=2RB,内有以B线圈作为理想边界的匀强磁场,若磁场均匀减小,则A、B环中感应电动势EA:EB与产生的感应电流IA:IB分别是()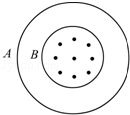
A.EA:EB=1:1;IA:IB=1:2 B.EA:EB=1:2;IA:IB=1:2
C.EA:EB=1:4;IA:IB=2:1 D.EA:EB=1:2;IA:IB=1:4
如图为一逻辑电路,根据电路图完成它的真值表.其输出端从上到下排列的结果正确的是()

| A.0 0 1 0 | B.0 0 1 1 |
| C.1 0 1 0 | D.0 0 0 1 |
如图所示,直线a为某电源与可变电阻连接成闭合电路时的路端电压U与干路电流I的关系图象,直线b为电阻R两端电压的U与通过它的电流I的图象,用该电源和该电阻组成闭合电路时,电源的输出功率和电源的效率分别为()
| A.4 W、33.3% | B.2 W、33.3% |
| C.4 W、67% | D.2 W、67% |