如图，等量异种点电荷，固定在水平线上的M、N两点上，有一质量为m、电荷量为＋q（可视为点电荷）的小球，固定在长为L的绝缘轻质细杆的一端，细杆另一端可绕过O点且与MN垂直的水平轴无摩擦地转动，O点位于MN的垂直平分线上距MN为L处。现在把杆拉起到水平位置，由静止释放，小球经过最低点B时速度为v，取O点电势为零，忽略q对等量异种电荷形成电场的影响。求：
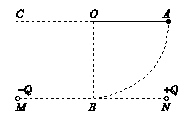
(1)小球经过B点时对杆的拉力大小
(2)在＋Q、－Q形成的电场中，A点的电势φA
(3)小球继续向左摆动，经过与A等高度的C点时的速度大小
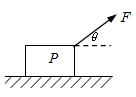
如图所示，质量为m=4.0kg的物体P静止在粗糙水平面上，与水平面间的动摩擦因数为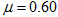
。现用与水平面成
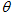=370、大小为20N的恒力F拉该物体，求物体P此时所受的支持力和摩擦力的大小。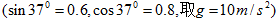
某物体做匀加速直线运动，通过一段位移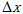
所用的时间为t1，紧接着通过下一段位移
所用的时间为t2。求物体运动的加速度大小和通过第一段位移的初速度的大小。
在xoy平面内存在着如图所示的电场和磁场，其中二、四象限内电场方向与y轴平行且相反，大小为E，一、三象限内磁场方向垂直平面向里，大小相等．一个带电粒子质量为m，电荷量为q，从第四象限内的P（L，﹣L）点由静止释放，粒子垂直y轴方向进入第二象限，求：
（1）磁场的磁感应强度B；
（2）粒子第二次到达y轴的位置；
（3）粒子从释放到第二次到达y轴所用时间．
如图所示，质量MA=2m的直杆A悬于离地面很高处，杆A上套有质量MB=m的小环B．将小环B由静止释放，环做加速度a=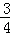
g的匀加速运动．经过时间t后，将杆A上方的细线剪断，杆A开始下落．杆A足够长，环B始终未脱离杆A，不计空气阻力，已知重力加速度为g，求：
（1）杆A刚下落时的加速度a′；
（2）在小环B下落的整个过程中，环B对杆A所做的功W；
（3）在小环B下落的整个过程中，系统产生的热量Q．
如图，一个质量为0.6kg 的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧时无机械能损失）．已知圆弧的半径R=0.3m，θ=60°，小球到达A点时的速度 v=4m/s．（取g=10m/s2）
求：（1）小球做平抛运动的初速度v0；
（2）P点与A点的水平距离和竖直高度；
（3）小球到达圆弧最高点C时速度和对轨道的压力．