如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m 1 的小球静止在轨道最低点,另一质量为m 2 的小球(两小球均可视为质点)从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m 1 发生碰撞并粘在一起.求 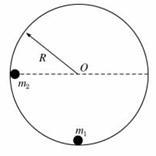
⑴小球m 2 刚要与m 1 发生碰撞时的速度大小;
⑵碰撞后,m 1 m 2 能沿内壁运动所能达到的最大高度(相对碰撞点).
一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车做匀速直线运动.司机发现其正要通过正前方高山悬崖下的隧道,于是鸣笛,经时间t1后听到回声;听到回声再行驶△t时间后,司机第二次鸣笛,又经时间t2后,听到回声.已知声音在空中的传播速度为v0.
(1)请根据以上条件推导客车速度的表达式。
(2)若此高速公路的最高限速为vm=120km/h,声音在 空中的传播速度为v0=340m/s,测得t1=6,6s,t2=3,4s,△t=12s,请判断此客车是否超速。
空中的传播速度为v0=340m/s,测得t1=6,6s,t2=3,4s,△t=12s,请判断此客车是否超速。
太阳的能量来自下面的反应:四个质子(氢核)聚变成一个毩粒子,同时发射两个正电子,若太阳辐射能量的总功率为P,质子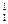 H、氦核
H、氦核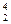 He、正电子
He、正电子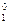 e的质量分别为mp、mα、me,真空中的光速为c,求:
e的质量分别为mp、mα、me,真空中的光速为c,求:
(1)写出核反应方程式.
(2)核反应所释放的能量△E.
(3)1s内参与上述热核反应的质子数目.
(3-5)
已知氘核的质量为2.0136u,中子质量为1.0087u,氦3( He)的质量为3.0150u.
He)的质量为3.0150u.
(1)写出两个氘核聚变生成氦3的方程;
(2)聚变放出的能量;
(3)若两个氘核以相同的动能Ek=0.35MeV正碰,求碰撞后生成物的动能.
(4)一群处于基态的氢原子,如果受到能量为En的光子照射后能辐射3种不同频率的光;如果受到能量为Em的光子照射后能辐射6种不同频率的光.已知氢原子的能级如图所示,则 ( )
( ) 
A.En=12.09eV,Em=12.75eV
B.En=1.5leV,Em=O.85eV
C.En=12.09eV,Em=13.06eV
D.En=1.5leV,Em=0.54ev
(5)光滑水平面上,用弹簧相连接的质量均为2kg的A、B两物体都以V0=6m/s速度向右运动。弹簧处于原长。质量为4kg的物体C静止在前方,如图所示,B与C发生相碰后合在一起运动,在以后的运动中,
①弹簧的弹性势能最大值为多少?
②弹性势能最大时,A的速度是多少?
(3-4)
(1)光线以某一入射角从空气射入折射率为 的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为 的某液体射入空气中正好发生全反射,入射角α等于___________________.
的某液体射入空气中正好发生全反射,入射角α等于___________________.
(2)如图所示,沿波的传播方向上有间距为1m的13个质点a.b.c.d.e.f.g.h.I.j.k.l.m,它们均静止在各自的平衡位置。一列横波以1m/s的速度水平向右传播,在t=0时刻到达质点a,且a开始由平衡位置向上振动,在t=1s时刻,质点a第一次达到最高点,求:
①这列波的波长和周期;
②从a开始振动,经过多长时间d点第一次向下达到最大位移;
③在上图中画出d点第一次向下达到最大位移时的波形图象。
(3-3)
(1)1968年,托雷一坎永号油轮在英吉利海峡触礁,有大约8万吨原油泄漏,污染了英国100多千米的海岸线,使25000只海鸟死亡。石油流入海中,危害极大。在海洋中泄漏m=1t原油可覆盖S=12km2的海面,试估算油膜厚度是原油的分子直径的多少倍?(设原油密度为ρ=0.91×103kg/m3,保留一位有效数字,分子直径的数量级D=10-10m)
(2)如图所示,一根足够长的两端开口的粗细均匀的直管,竖直插入很大的水银槽中。有个质量不计的横截面积S=1cm2的活塞A,在管中封闭一段长L=10cm的理想气体。开始时A处于静止状态。现在用力F竖直向上缓慢拉动活塞A,不计管壁对A的摩擦。当F=2N时,A再次静止。设整个过程中环境温度不变,外界大气压p0=1.0×105Pa(约为75cmHg),求:
①A再次静止时的气体压强P2;
②A再次静止时的气体长度L2;
③在此过程中活塞A上升的距离h。