某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校 学年高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在
学年高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在 分下的学生后,共有男生
分下的学生后,共有男生 名,女生
名,女生 名,现采用分层抽样的方法,从中抽取了
名,现采用分层抽样的方法,从中抽取了 名学生,按性别分为两组,并将两组学生成绩分为
名学生,按性别分为两组,并将两组学生成绩分为 组,得到如下所示频数分布表.
组,得到如下所示频数分布表.
| 分数段 |
 |
 |
 |
 |
 |
 |
| 男 |
 |
 |
 |
 |
 |
 |
| 女 |
 |
 |
 |
 |
 |
 |
(1)估计男、女生各自的平均分(同一组数据用该级区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定 分以上者为优分(含
分以上者为优分(含 分),请你根据已知条件作出
分),请你根据已知条件作出 列联表,并判断是否有
列联表,并判断是否有 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

已知 (其中e为自然对数的底数)。
(其中e为自然对数的底数)。
(1)求函数
 上的最小值;
上的最小值;
(2)是否存在实数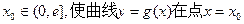 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出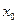 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
设函数 是定义域为R上的奇函数。
是定义域为R上的奇函数。
(1)求 的值.
的值.
(2)若 上的最小值为—2,求m的值。
上的最小值为—2,求m的值。
在曲线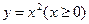 上有点A
上有点A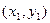 和点B
和点B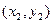 ,且
,且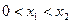 ,在A,B处的切线分别为
,在A,B处的切线分别为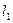 和
和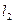 ,记
,记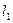 与曲线以及
与曲线以及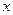 轴所围图形面积为
轴所围图形面积为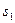 ,
,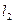 与曲线以及
与曲线以及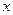 轴所围图形面积为
轴所围图形面积为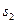 ,
,
(1)若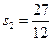 ,求过切点B的切线方程。
,求过切点B的切线方程。
(2)若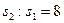 ,求
,求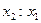 的值。
的值。
设函数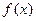 =
=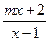 的图象的对称中心为点(1,1).
的图象的对称中心为点(1,1).
(1)求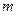 的值;
的值;
(2)若直线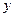 =
=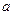 (
(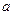 ∈R)与
∈R)与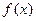 的图象无公共点,且
的图象无公共点,且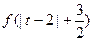 <2
<2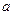 +
+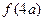 ,求实数
,求实数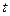 的取值范围.
的取值范围.
、已知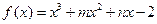 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数 的图象关于y轴对称。
的图象关于y轴对称。
(1)求m,n的值及函数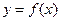 的单调区间;
的单调区间;
(2)若a>0,求函数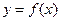 在区间
在区间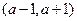 内的极值。
内的极值。