下面有五个命题:
①函数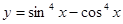 的最小正周期是
的最小正周期是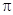 ;
;
②终边在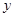 轴上的角的集合是
轴上的角的集合是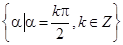 ;
;
③函数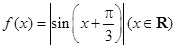 ,在区间
,在区间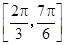 上是增函数;
上是增函数;
④若动直线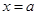 与函数
与函数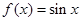 和
和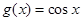 的图像分别交于
的图像分别交于 两点,则
两点,则 的最大值为1.
的最大值为1.
其中真命题的序号是 。
在直角坐标系xOy中, 以原点为极点, x轴的正半轴为极轴建立极坐标系, 记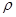 为极径,
为极径, 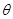 为极角, 圆C:
为极角, 圆C: 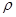 ="3" cos
="3" cos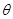 的圆心C到直线
的圆心C到直线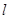 :
: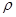 cos
cos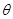 =2的距离为.
=2的距离为.
如图, 已知圆O的半径为3, AB与圆D相切于A, BO与圆O相交于C, BC ="2," 则△ABC的面积为. 
观察下面两个推理过程及结论:
(1) 若锐角A, B, C满足A+B+C= , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: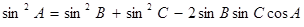
(2) 若锐角A, B, C满足A+B+C= , 则
, 则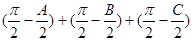 =
= , 以
, 以 分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
得到的等式: 则:若锐角A, B, C满
则:若锐角A, B, C满
足A+B+C= , 类比上面推理方法, 可以得到一个等式是.
, 类比上面推理方法, 可以得到一个等式是.
给出下列命题:
①在锐角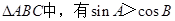 ;
;
②函数 图象关于点
图象关于点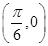 对称;
对称;
③在 , 则
, 则 必为等边三角形;
必为等边三角形;
④在同一坐标系中, 函数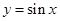 的图象和函数
的图象和函数 的图象有三个公共点.
的图象有三个公共点.
其中正确命题的序号是______(写出所有正确命题的序号).
执行如图所示的程序框图, 若输入a的值为2, 则输出的p值是. 