如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连。小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道。小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为l.8R。求: (在运算中,根号中的数值无需算出)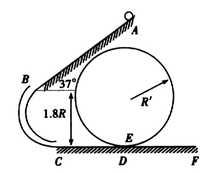
(1)小球滑到斜面底端C时速度的大小。
(2)小球刚到C时对轨道的作用力。
(3)要使小球在运动过程中不脱离轨道,竖直圆周轨道的半径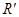 应该满足什么条件?
应该满足什么条件?
目前我国动车组在广泛使用。假设动车轨道为直线,动车制动时的阻力为重力的0.1倍。(g=10m/s2)
(1)如果动车司机发现前方450m处有故障车已经停车,要使动车不发生追尾,则动车运行速度不能超过多少?(不考虑司机的反应时间)
(2)如果动车运行的速度为252km/h,当动车司机前方2464m处有故障车已经停车,经反应后制动减速,为了确保列车不发生追尾,问动车司机反应时间不得超过多少?
如图所示,在光滑的水平面上停放着小车B,车上左端有一可视为质点的小物块A,A和B之间的接触面前一段光滑,后一段粗糙,且后一段的动摩擦因数μ=0.4,小车长L=2 m,A的质量 mA=1 kg,B的质量mA=4 kg,现用12 N的水平力F向左拉动小车,当A到达B的最右端时,两者速度恰好相等,求:
(1)A在B的光滑和粗糙部分运动时,两个物体的加速度;
(2)A和B间光滑部分的长度.(g取10 m/s2)
如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2 m/s的速率运行.现把一质量为m=1 kg的工件(可看为质点)轻轻放在传送带的底端,经时间t=1.9 s,工件被传送到h=1.5 m的高处,并取得了与传送带相同的速度,取g=10 m/s2.求: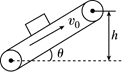
(1)工件与传送带之间的滑动摩擦力F;
(2)工件与传送带之间的相对位移Δs.
一辆值勤的警车停在一条直公路的道边,当警员发现从他旁边以v=8 m/s的速度匀速行驶的货车有违章行为时,决定前去追赶,经Δt=2.5 s警车发动起,以加速度a=2 m/s2做匀加速运动,若警车能达到的最大速度是vm=12 m/s,达到最大速度后以该速度匀速运动.试问:
(1)警车发动起后要多长时间才能追上违章的货车?
(2)警车在追赶货车的过程中,两车间的最大距离是多少?
如图所示,质量M=8 kg的小车放在光滑的水平面上,在小车左端加一水平推力F=8 N,当小车向右运动的速度达到1.5 m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2 kg的小物块,小物块与小车间的动摩擦因数μ=0.2,当二者达到相同速度时,物块恰好滑到小车的最左端。取g=10 m/s2。则: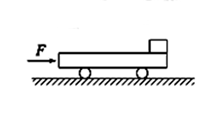
(1)小物块放上后,小物块及小车的加速度各为多大?
(2)小车的长度L是多少?