设定义在R上的函数f(x)对于任意x,y都有f(x+y)=f(x)+f(y)成立,且f(1)=﹣2,当x>0时,f(x)<0.
(1)判断f(x)在R上的单调性,并加以证明;
(2)当﹣2015≤x≤2015时,不等式f(x)≤k恒成立,求实数k的取值范围.
(本小题满分12分)
已知直线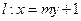 过椭圆
过椭圆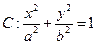 的右焦点
的右焦点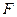 ,抛物线:
,抛物线: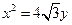 的焦点为椭圆
的焦点为椭圆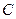 的上顶点,且直线
的上顶点,且直线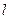 交椭圆
交椭圆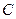 于
于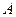 、
、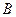 两点,点
两点,点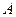 、
、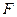 、
、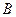 在直线
在直线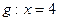 上的射影依次为点
上的射影依次为点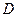 、
、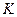 、
、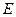 .
.
(1)求椭圆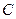 的方程;
的方程;
(2)若直线l交y轴于点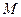 ,且
,且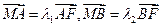 ,当
,当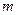 变化时,探求
变化时,探求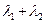 的值是否为定值?若是,求出
的值是否为定值?若是,求出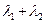 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接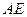 、
、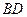 ,试探索当
,试探索当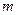 变化时,直线
变化时,直线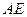 与
与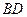 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
(本小题满分12分)已知函数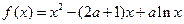
(1)当 时,求函数
时,求函数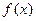 的单调增区间,求函数
的单调增区间,求函数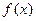 区间
区间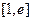 上的最小值;
上的最小值;
(2)设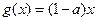 ,若存在
,若存在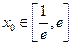 ,使得
,使得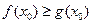 成立,求实数
成立,求实数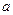 的取值范围。
的取值范围。
(本小题满分12分) 如图,在三棱锥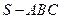 中,
中,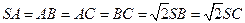 ,
,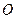 为
为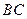 的中点.
的中点.
(1)求证: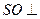 面
面 ;
;
(2)求异面直线 与
与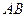 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)已知圆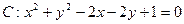 ,直线
,直线 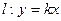 ,
,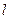 与圆
与圆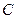 交与
交与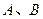 两点,点
两点,点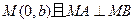 .
.
(1)当 时,求
时,求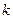 的值;
的值;
(2)当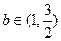 时,求
时,求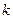 的取值范围.
的取值范围.
(本小题满分10分)
已知函数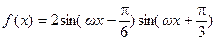 (其中
(其中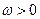 ,
,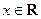 )的最小正周期为
)的最小正周期为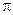 .
.
(1)求 的值;
的值;
(2)在△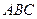 中,若
中,若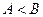 ,且
,且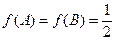 ,求
,求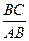 .
.