在某星球上，宇航员做了一个实验：让质量为m="1." 0 kg的小滑块以v0="6" m/s的初速度从倾角为θ= 530的斜面AB的顶点A滑下，到达B点后与垂直斜面的挡板碰撞，不计碰撞时的机械能损失．滑块与斜面间的动摩擦因数为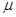
=" 0." 5，测得A点离B点所在水平面的高度为h=3m，最终物块在斜面上通过的路程s =" 20" m.已知sin 530 =" 0." 8 ，cos 530="0." 6，不计该星球的自转以及其他星球对它的作用．
(1)求该星球表面的重力加速度g；
(2)若测得该星球的半径为R=6
106 m，则该星球的第一宇宙速度为多大？
(3)取地球半径Ro＝6.4106m，地球表面的重力加速度g0＝10 m/s2，求该星球的平均密度与地球的平均密度之比
．
轻杆长2L，A端连在固定转动轴上，B端固定一个质量为2m的小球，中点C固定一个质量为m的小球。AB杆可以绕A在竖直平面内自由转动。现将杆从水平位置，如图所示，由静止释放，不计各处摩擦与空气阻力，试求：AB杆转到竖直位置瞬时，角速度ω多大？
(9分)如图所示，一传送皮带与水平面夹角为
，以2m/s的恒定速度顺时针运行。现将一质量为10kg的工件轻放于底端，经一段时间送到高2m的平台上，工件与皮带间的动摩擦因数为
，求带动皮带的电动机由于传送工件多消耗的电能。（g取10m/s2）
飞镖是一种体育运动。镖以水平速度或斜向上的速度飞出并击中靶盘。若运动员从同一位置将两只镖水平射出，两只镖落在竖直盘上且与盘面的夹角分别为
和
，两只镖落地点之间的竖直距离为d，如图甲所示。试求镖射出点到镖盘的水平距离。
如图所示，一质量为m的小物块沿竖直放置的半径为R的
圆弧形槽的上端往下滑，初速度为
，滑到槽底末端的速度为
，求物块在下滑过程中产生的热量。
(9分)如图所示，在距离一质量为M、半径为R、密度均匀的球体R远处有一质量为m的质点，此时M对m的万有引力为
。当从M中挖去一半径为
的球体后，剩下部分对m的万有引力为
，则
多大？