“神舟”六号载人飞船在空中环绕地球做匀速圆周运动,某次经过赤道的正上空时,对应的经度为θ1,飞船绕地球转一圈后,又经过赤道的正上空,此时对应的经度为θ2(θ1、θ2均表示弧度).已知地球半径为R,地球表面的重力加速度为g,地球自转的周期为T0.求飞船运行的圆周轨道离地面高度h的表达式.(用θ1、θ2、T0、g和R表示).
(选修模块3—3)(1)若一气泡从湖底上升到湖面的过程中温度保持不变,则在此过程中关于气泡中的气体,下列说法正确的是()。(填写选项前的字母)
(A)气体分子间的作用力增大(B)气体分子的平均速率增大
(C)气体分子的平均动能减小(D)气体组成的系统地熵增加
(2)若将气泡内的气体视为理想气体,气泡从湖底上升到湖面的过程中,对外界做了0.6J的功,则此过程中的气泡(填“吸收”或“放出”)的热量是 J。气泡到达湖面后,温度上升的过程中,又对外界做了0.1J的功,同时吸收了0.3J的热量,则此过程中,气泡内气体内能增加了 J。
(3)已知气泡内气体的密度为1.29kg/ ,平均摩尔质量为0.29kg/mol。阿伏加德罗常数
,平均摩尔质量为0.29kg/mol。阿伏加德罗常数 ,取气体分子的平均直径为
,取气体分子的平均直径为 ,若气泡内的气体能完全变为液体,请估算液体体积与原来气体体积的比值。(结果保留一位有效数字)。
,若气泡内的气体能完全变为液体,请估算液体体积与原来气体体积的比值。(结果保留一位有效数字)。
如图所示,一个被x轴与曲线方程y=0.2sin  x(m)所围的空间中存在着匀强磁场.磁场方向垂直纸面向里,磁感应强度B=0.2 T.正方形金属线框的边长是L=0.2 m,电阻是R=0.1 Ω,它的一边与x轴重合,在拉力F的作用下,以v=10 m/s的速度水平向右匀速运动.试求:
x(m)所围的空间中存在着匀强磁场.磁场方向垂直纸面向里,磁感应强度B=0.2 T.正方形金属线框的边长是L=0.2 m,电阻是R=0.1 Ω,它的一边与x轴重合,在拉力F的作用下,以v=10 m/s的速度水平向右匀速运动.试求:
(1)拉力F的最大功率是多少?
(2)拉力F要做多少功才能把线框拉过磁场区?
(3)有位同学在老师的帮助下算出了曲线与x轴所围的面积为 m2.请你再帮他算出线框右边框通过磁场区域的过程中通过线框某一截面的电荷量.(结果保留两位有效数字)
m2.请你再帮他算出线框右边框通过磁场区域的过程中通过线框某一截面的电荷量.(结果保留两位有效数字)
(16分)一矩形线圈abcd放置在如图所示的有理想边界的匀强磁场中(OO′的左边有匀强磁场,右边没有),线圈的两端接一只灯泡.已知线圈的匝数n=100,电阻r=1.0 Ω,ab边长L1=0.5 m,ad边长L2=0.3 m,小灯泡的电阻R=9.0 Ω,磁场的磁感应强度B=1.0×10-2 T.线圈以理想边界OO′为轴以角速度ω=200 rad/s按如图10-1-22所示的方向匀速转动(OO′轴离ab边距离为 L2),以如图所示位置为计时起点.求:
L2),以如图所示位置为计时起点.求:
(1)在0~ 的时间内,通过小灯泡的电荷量;
的时间内,通过小灯泡的电荷量;
(2)画出感应电动势随时间变化的图象(以abcda方向为正方向,至少画出一个完整的周期);
(3)小灯泡消耗的电功率.
两个完全相同的电热器,分别通过如图a和b所示的电流最大值相等的方波交变电流和正弦交变电流,则这两个电热器的电功率之比Pa∶Pb等于多少?
(16分)一个电阻为r、边长为L的正方形线圈abcd共N匝,线圈在磁感应强度为B的匀强磁场中绕垂直于磁感线的轴OO′以如图所示的角速度ω匀速转动,外电路电阻为R.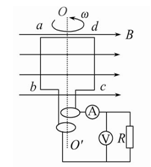
(1)在图中标出此刻线圈感应电流的方向.
(2)线圈转动过程中感应电动势的最大值有多大?
(3)线圈平面与磁感线夹角为60°时的感应电动势为多大?
(4)设发电机由柴油机带动,其他能量损失不计,线圈转一周,柴油机做多少功?
(5)从图示位置开始,线圈转过60°的过程中通过R的电量是多少?
(6)图中电流表和电压表的示数各是多少?