如图所示，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动.
（1）如果P、Q同时出发，几秒钟后，可使△PCQ的面积为8平方厘米？
（2）点P、Q在移动过程中，是否存在某一时刻，使得△PCQ的面积等于△ABC的面积的一半.若存在，求出运动的时间；若不存在，说明理由.
仔细观察，探索规律：
（x－1）（x+1）=x2－1
（x－1）（x2+x+1）=x3－1
（x－1）（x3+x2+x+1）=x4－1
（x－1）（x4+x3+x2+x+1）=x5－1
……
（1）试求25+24+23+22+2+1的值；
（2）写出22006+22005+22004+…+2+1的个位数．
我们在计算（2+1）（22+1）（24+1）（28+1）（216+1）（232+1）时，发现直接运算很麻烦，如果在算式前乘以（2－1），即1，原算式的值不变，而且还使整个算式能用乘法公式计算．解答过程如下：
原式=（2－1）（2+1）（22+1）（24+1）（28+1）（216+1）（232+1）
=（22－1）（22+1）（24+1）（28+1）（216+1）（232+1）
=（24－1）（24+1）（28+1）（216+1）（232+1）
=……=264－1
你能用上述方法算出（3+1）（32+1）（34+1）（38+1）（316+1）的值吗？请试试看!
综合提高
解方程：（－3x－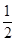
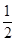）（－3x）=x（9x－
）
利用平方差公式计算：20052－2004×2006
利用平方差公式计算：200.2×199.8