如图所示是一列横渡上A、B两质点的振动图象,两质点沿波的传播方向上的距离△x=4.0m.求这列波的波速。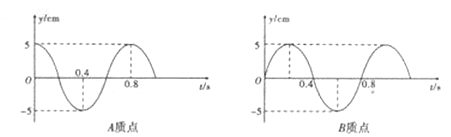
如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R,重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求
(1)粘合后的两球从飞出轨道到落地的时间t;
(2)小球A冲进轨道时速度v的大小。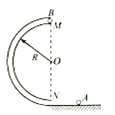
如图所示,长度为 的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略)。在水平拉力F的作用下,轻绳与竖直方向的夹角为
的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略)。在水平拉力F的作用下,轻绳与竖直方向的夹角为 ,小球保持静止,画出此时小球的受力图,并求力F的大小; 由图示位置无初速度释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。
,小球保持静止,画出此时小球的受力图,并求力F的大小; 由图示位置无初速度释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。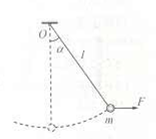
如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度 ="4" m/s,g取10
="4" m/s,g取10 。
。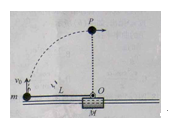
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向。
(2)若解除对滑块的锁定,试求小球通过最高点时的速度大小。
在满足(2)的条件下,试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
26.装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击。通过对一下简化模型的计算可以粗略说明其原因。
质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿。现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离水平放置,如图所示。若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度。设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞不计重力影响。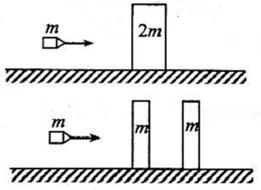
(2011·菏泽模拟)(20分)如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4 m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处有一质量m=1 kg的小球由静止下滑,经过B、C两点后从D点斜抛出去,最后落在地面上的S点时的速度大小vS=8 m/s,已知A点距地面的高度H=10 m,B点距地面的高度h=5 m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10 m/s2, cos53°=0.6,求: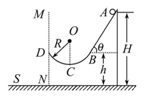
(1)小球经过B点时的速度为多大?
(2)小球经过圆弧轨道最低处C点时受到的支持力为多大?
(3)小球从D点抛出后,受到的阻力Ff与其瞬时速度方向始终相反,求小球从D点至S点的过程中阻力所做的功.