(本小题满分12分)已知曲线 在点
在点 处的切线的斜率为1.
处的切线的斜率为1.
(1)若函数f(x)的图象在 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(2)当 时,不等式
时,不等式 恒成立,求a的取值范围.
恒成立,求a的取值范围.
1)设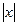 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤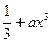 ;
;
(2)设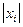 ≤1,
≤1, ,求证:
,求证: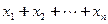 ≤
≤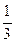
如图:空间四边形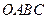 中,点
中,点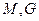 分别是
分别是 的中点.设
的中点.设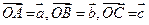
(1)用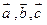 表示向量
表示向量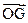 .
.
(2)若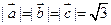 ,且
,且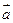 与
与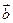 、
、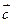 夹角的余弦值均为
夹角的余弦值均为 ,
,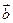 与
与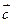 夹角为600,求
夹角为600,求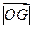
已知抛物线的顶点在坐标原点,焦点F在x轴的正半轴上,且F到抛物线的准线的距离为p.
(1) 求出这个抛物线的方程;
(2)若直线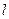 过抛物线的焦点F,交抛物线与A、B两点, 且
过抛物线的焦点F,交抛物线与A、B两点, 且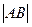 ="4p" ,求直线
="4p" ,求直线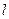 的方程.
的方程.
如果双曲线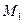 与双曲线
与双曲线 的焦点在同一坐标轴上且它们的虚轴长和实轴长的比值相等,则称他们为平行双曲线.已知双曲线M与双曲线
的焦点在同一坐标轴上且它们的虚轴长和实轴长的比值相等,则称他们为平行双曲线.已知双曲线M与双曲线 为平行双曲线,且点(2,0)在双曲线M上.
为平行双曲线,且点(2,0)在双曲线M上.
(1)求双曲线M的方程;
(2) 设P是双曲线M上的任一点,点A的坐标为(3,0),求|PA|的最小值.
已知椭圆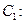
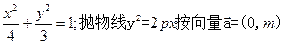
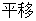 ,
,
得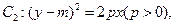 且
且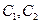 的公共弦
的公共弦 过椭圆
过椭圆 的右焦点。
的右焦点。
⑴当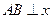 轴时,求
轴时,求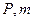 的值,并判断抛物线
的值,并判断抛物线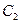 的焦点是否在直线
的焦点是否在直线 上;
上;
⑵若 ,且抛物线
,且抛物线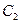 的焦点在直线
的焦点在直线 上,求
上,求 的值及直线AB的方程。
的值及直线AB的方程。