(本小题满分12分)设函数 .
.
(Ⅰ)若 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)若 ,且
,且 在
在 上的最小值为
上的最小值为 ,求
,求 在该区间上的最大值.
在该区间上的最大值.
如图,已知四棱锥 ,底面
,底面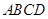 为菱形,
为菱形, 平面
平面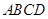 ,
,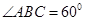 ,
,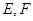 分别是
分别是 的中点.
的中点.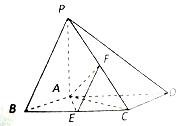
(Ⅰ)证明: ;
;
(Ⅱ)若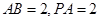 ,求二面角
,求二面角 的余弦值.
的余弦值.
甲、乙两人共同抛掷一枚硬币,规定硬币正面朝上甲得1分,否则乙得1分,先积得3分者获胜,并结束游戏.
(Ⅰ)求在前3次抛掷中甲得2分,乙得1分的概率;
(Ⅱ)若甲已经积得2分,乙已经积得1分,求甲最终获胜的概率;
(Ⅲ)用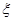 表示决出胜负抛硬币的次数,求
表示决出胜负抛硬币的次数,求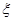 的分布列及数学期望.
的分布列及数学期望.
在数列 中,
中,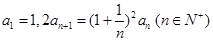 .
.
(Ⅰ)证明数列 成等比数列,并求
成等比数列,并求 的通项公式;
的通项公式;
(Ⅱ)令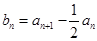 ,求数列
,求数列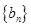 的前
的前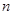 项和
项和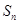 .
.
已知函数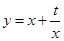 有如下性质:如果常数
有如下性质:如果常数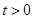 ,那么该函数在
,那么该函数在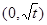 上是减函数,在
上是减函数,在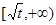 上是增函数.
上是增函数.
(1)已知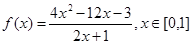 ,利用上述性质,求函数
,利用上述性质,求函数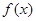 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数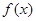 和函数
和函数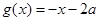 ,若对任意
,若对任意 ∈[0,1],总存在
∈[0,1],总存在 ∈[0,1],使得
∈[0,1],使得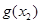 =
=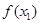 成立,求实数
成立,求实数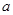 的值.
的值.
已知 是奇函数(其中
是奇函数(其中 ).
).
(1)求 的值;
的值;
(2)判断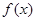 在
在 上的单调性并证明;
上的单调性并证明;
(3)当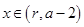 时,
时,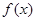 的取值范围恰为
的取值范围恰为 ,求
,求 与
与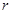 的值.
的值.