(本小题满分10分)选修4-1:几何证明选讲
如图,圆周角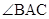 的平分线与圆交于点
的平分线与圆交于点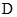 ,过点
,过点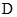 的切线与弦
的切线与弦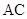 的延长线交于点
的延长线交于点 ,
, 交
交 于点
于点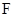 .
.
(1)求证: ;
;
(2)若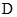 ,
, ,
,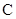 ,
,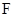 四点共圆,且
四点共圆,且 ,求
,求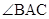 .
.
已知复数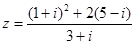 .
.
(1)求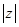 ;
;
(2)若 ,求实数
,求实数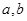 的值.
的值.
【附加题】(5分,计入总分,但总分不超过100分):B班同学做,A班做了也没分L
求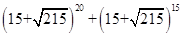 的十进制表达式中的个位数字.
的十进制表达式中的个位数字.
【附加题】(5分,计入总分,但总分不超过100分):A班同学做,B班做了也没分L
设三角形的三边长分别是整数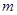 ,
,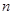 ,
,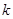 ,且
,且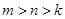 ,已知
,已知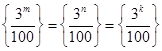 ,其中
,其中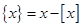 ,而
,而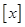 表示不超过
表示不超过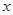 的最大整数,求这种三角形周长的最小值.
的最大整数,求这种三角形周长的最小值.
已知椭圆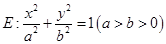 的离心率
的离心率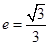 ,它的上顶点为
,它的上顶点为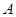 ,左、右焦点为
,左、右焦点为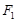 ,
,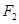 ,直线
,直线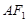 ,
,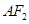 分别交椭圆于点
分别交椭圆于点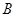 ,
,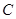 .
.
(1)判断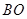 是否平分线段
是否平分线段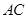 ,说明理由;
,说明理由;
(2)若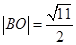 ,
,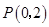 ,过
,过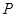 的动直线
的动直线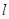 交椭圆于
交椭圆于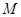 ,
,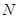 两点,在线段
两点,在线段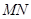 上取点
上取点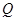 ,使
,使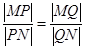 .
.
①写出椭圆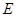 的方程;
的方程;
②求点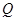 的轨迹方程.
的轨迹方程.
设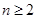 ,
,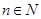 ,
,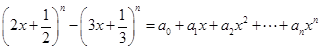 .
.
(1)求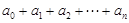 ;
;
(2)记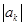 (
(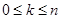 )的最小值为
)的最小值为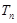 .
.
①求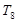 ;
;
②若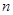 为奇数,求
为奇数,求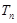 .
.