(本小题满分13分)一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为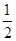 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列和数学期望E(X).
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
已知Sn是等比数列{an}的前n项和,S4,S2,S3成等差数列,且a2+a3+a4=-18.
(1)求数列{an}的通项公式;
(2)是否存在正整数n,使得Sn≥2 013?若存在,求出符合条件的所有n的集合;若不存在,说明理由.
设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,求x的取值范围.
已知椭圆C: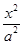 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,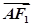 ·
· =0,3|
=0,3| |·|
|·|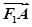 |=-5
|=-5 ·
·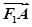 ,|
,| |=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
|=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
(1)求椭圆C的方程;
(2)线段OF2(O为坐标原点)上是否存在点M(m,0),使得 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A,B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
设椭圆C: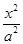 +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为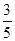 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.