如图（1），OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：
（1）如图（2），在△ABC中，∠ACB是直角，∠B＝60°， AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请你判断并写出FE与FD之间的数量关系；
（2）如图（3），在△ABC中，如果∠ACB不是直角，而（1）中的其他条件不变，在（1）中所得结论是否仍然成立？请说明理由．
课堂上王老师给大家出了这样一道题，“当
时，求代数式
的值”，小明一看，“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？请写出具体过程.
人在运动时的心跳速率和人的年龄有关,如果用
表示一个人的年龄,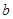
表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么有
,请问:一个45岁的人某时心跳次数达到了122次,他有危险吗?
解方程：（1）6x=3x－12 （2）
化简：（1）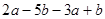
（2）
（1）如图①，已知C是线段AB上一点，分别以AC、BC为边长在AB的同侧作等边△ADC与等边△CBE，试猜想AE与DB的大小关系，并证明.
（2）如图②，当等边△CBE绕点C旋转后，上述结论是否仍成立？若成立，请证明；若不成立，请说明理由