如图所示，用一块长L1=2.5m的木板（木板下端有一底座高度与木板A、B相同）在墙和地面间架设斜面，斜面与水平地面的倾角θ可在0~60°间调节后固定。将质量m1=5kg的小物块从斜面顶端静止释放，为避免小物块与地面发生撞击，在地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为l=2m，质量均为m2=10kg（忽略小物块在转角处和底座运动的能量损失）。物块与斜面间的动摩擦因数μ=0.125，物块与木板间的动摩擦因数μ1=0.4，木板与地面间的动摩擦因数μ2=0.1（最大静摩擦力等于滑动摩擦力；重力加速度g=10m/s2）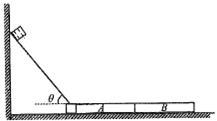
（1）当θ角增大到多少时，小物块能从斜面开始下滑？（用正切值表示）
（2）当θ增大到37°时，通过计算判断货物是否会从木板B的右端滑落？若能，求货物滑离木板B右端时的速度；若不能，求货物最终停在B板上的位置？（已知sin37°=0.6，cos37°=0.8）
一台直流电动机的额定电压为U=110V，电动机线圈的电阻R=0.5Ω，正常工作时通过的电流I=2A，若电动机正常运转1 min.求：
（1）电流所做的功；
（2）电动机线圈上产生的热量；
（3）电动机输出的机械能
如图所示，R1＝5Ω，R2＝9Ω。当开关S断开时，电流表的示数为I＝0.2A当开关S闭合时，电流表的示数为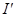
＝0.3A。（电流表内阻不计）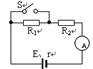
求：电源的电动势和内阻．
(12分)如图所示，有一个可视为质点的质量为m＝1 kg的小物块，从光滑平台上的A点以v0＝2 m/s的初速度水平抛出，到达C点时，恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道，最后小物块滑上紧靠轨道末端D点的质量为M＝3 kg的长木板．已知木板上表面与圆弧轨道末端切线相平，木板下表面与水平地面之间光滑，小物块与长木板间的动摩擦因数μ＝0.3，圆弧轨道的半径为R＝0.4 m，C点和圆弧的圆心连线与竖直方向的夹角θ＝60°，不计空气阻力，g取10 m/s2.求：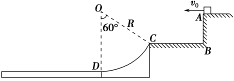
（1）小球到达C点时的速度
（2）小物块刚要到达圆弧轨道末端D点时对轨道的压力；
（3）要使小物块不滑出长木板，木板的长度L至少多大？
如图，一质量m=1×10-6kg，带电量q= -2×10-8C的微粒以初速度v0竖直向上从A点射入一水平向右的匀强电场，当微粒运动到比A高2cm的B点时速度大小也是v0，但方向水平，且AB两点的连线与水平方向的夹角为45º，g取10m/s2，求：
（1）AB两点间的电势差UAB；
（2）匀强电场的场强E的大小。
如图所示，轨道ABC被竖直地固定在水平桌面上，A距离水平地面高H＝0.75 m，C距离水平地面高h＝0.45 m．一质量m＝0.10 kg的小物块自A点从静止开始下滑，从C点以水平速度飞出后落在水平地面上的D点．现测得C、D两点的水平距离为l＝0.60 m．不计空气阻力，取g＝10 m/s2.求：
(1)小物块从C点飞出时速度的大小；
(2)小物块从A点运动到C点的过程中克服摩擦力做的功．