如图甲所示,质量相等大小可忽略的a、b两小球用不可伸长的等长轻质细线悬挂起来,使小球a在竖直平面内来回摆动,小球b在水平面内做匀速圆周运动,连接小球b的绳子与竖直方向的夹角和小球a摆动时绳子偏离竖直方向的最大夹角都为θ,运动过程中两绳子拉力大小随时间变化的关系如图乙中c、d所示.则下列说法正确的是( )

| A.图乙中直线d表示绳子对小球a的拉力大小随时间变化的关系 |
| B.图乙中曲线c表示绳子对小球a的拉力大小随时间变化的关系 |
| C.θ=45° |
| D.θ=60° |
如图所示,竖直平面内有一固定的光滑绝缘椭圆大环,水平长轴为AC,竖直短轴为ED。轻弹簧一端固定在大环的中心O,另一端连接一个可视为质点的带正电的小环,小环刚好套在大环上,整个装置处在一个水平向里的匀强磁场中.将小环从A点由静止释放,已知小环在A、D两点时弹簧的形变量大小相等。下列说法中错误的是( )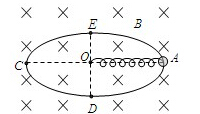
A.刚释放时,小球的加速度为重力加速度g
B. 小环的质量越大,其滑到D点时的速度将越大
C. 小环从A到运动到D,弹簧对小环先做正功后做负功
D. 小环一定能滑到C点
对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r处的电势为φ=kq/r(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为()
A.减少 |
B.增加 |
C.减少 |
D.增加 |
如右图所示,I,II分别是甲、乙两小球从同一地点沿同一直线运动的v-t图线,根据图线可以判断()
| A.甲、乙两小球做的是初速度方向相反的匀变速直线运动,加速度大小相同,方向相同 |
| B.两球在t=8s时相距最远 |
| C.两球在t=2s时刻速度相等 |
| D.两球在t=8s时相遇 |
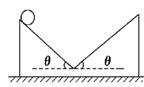
伽利略曾利用对接斜面研究“力与运动”的关系。如图所示,固定在水平地面上的倾角均为θ的两斜面,以光滑小圆弧相连接。左侧斜面顶端的小球与两斜面的动摩擦因数均为μ。小球从左侧顶端滑到最低点的时间为t1,滑到右侧最高点的时间为t2。规定两斜面连接处所在水平面为参考平面,则小球在这个运动过程中速度的大小v、加速度的大小a、动能Ek及机械能E随时间t变化的关系图线正确的是()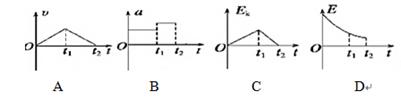
如图所示,一根轻杆两端各固定一个质量均为m的相同小球,用两根细绳悬挂在天花板上,虚线为竖直线,α=θ=30°,β=60°,则轻杆对A球的作用力为( )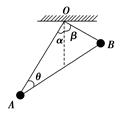
| A.mg | B. mg mg |
C.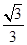 mg mg |
D.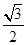 mg mg |