如图所示,一水平的浅色长传送带上放置一质量为m的煤块(可视为质点),煤块与传送带之间的动摩擦因数为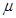 。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度
。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度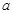 开始运动,当其速度达到
开始运动,当其速度达到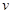 后,便以此速度作匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动,关于上述过程,以下判断正确的是(重力加速度为g)( )
后,便以此速度作匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动,关于上述过程,以下判断正确的是(重力加速度为g)( )

A.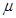 与 与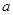 之间一定满足关系 之间一定满足关系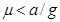 |
B.煤块从开始运动到相对于传送带静止经历的位移为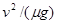 |
C.煤块从开始运动到相对于传送带静止经历的时间为 |
D.黑色痕迹的长度为 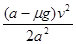 |
带电粒子进入云室会使云室中的气体电离,从而显示其运动轨迹。如图所示是在有匀强磁场云室中观察到的粒子的轨迹,a和b是轨迹上的两点,匀强磁场B垂直纸面向里。该粒子在运动时,其质量和电量不变,而动能逐渐减少,下列说法正确的是
| A.粒子先经过a点,再经过b点 |
| B.粒子先经过b点,再经过a点 |
| C.粒子带负电 |
| D.粒子带正电 |
有关氢原子光谱的说法,正确的是()
| A.氢原子的发射光谱是连续谱 |
| B.氢原子光谱说明氢原子只发出某些特定频率的光 |
| C.氢原子光谱说明氢原子的能级是分立的 |
| D.氢原子光谱线的频率与氢原子能级的能量差无关 |
如图所示,OO'是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于OO'轴等距且平行的两束不同单色细光束,从玻璃射出后相交于OO'下方的P点,由此可以得出的结论
| A.在玻璃中,A光比B光的速度小 |
| B.玻璃对A光的折射率比对B光的折射率小 |
| C.空气中,A光的波长比B光的波长长 |
| D.A光的光子能量比B光的光子能量大 |
质量为M,长为L的小车静止在光滑的水平面上,质量为m的小物块放在小车的最左端,现有一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动。物块和小车之间的摩擦力为f。经过时间t,小车的位移为s,物块刚好滑到小车的最右端。则以下说法正确的是
| A.此时物块的动能为(F-f)(s+L) |
| B.此时物块的动量为Ft |
| C.这一过程中物块和小车增加的动能为Fs |
| D.这一过程中物块和小车减少的机械能为fL |
一个静止的天然放射性元素的原子核在匀强磁场中发生衰变,所产生的新核和所放出的粒子的运动方向均垂直于磁场方向,如下图所示,能正确反映其轨道的可能是