已知函数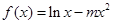 ,
,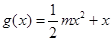 (
( ),令
),令 .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若关于x的不等式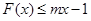 恒成立,求整数m的最小值.
恒成立,求整数m的最小值.
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
| 偏高 |
2 |
 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(I)试确定 、
、 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
在△ABC中, 为三个内角
为三个内角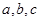 为三条边,
为三条边, 且
且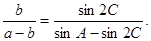
(I)判断△ABC的形状;
(II)若 ,求
,求 的取值范围.
的取值范围.
设数列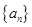 的各项均为正数.若对任意的
的各项均为正数.若对任意的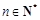 ,存在
,存在 ,使得
,使得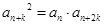 成立,则称数列
成立,则称数列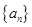 为“Jk型”数列.
为“Jk型”数列.
(1)若数列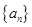 是“J2型”数列,且
是“J2型”数列,且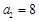 ,
, ,求
,求 ;
;
(2)若数列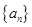 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列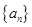 是等比数列.
是等比数列.
如图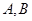 是单位圆
是单位圆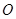 上的点,
上的点, 分别是圆
分别是圆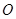 与
与 轴的两交点,
轴的两交点, 为正三角形.
为正三角形.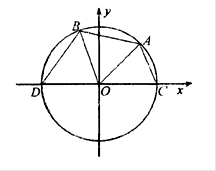
(1)若 点坐标为
点坐标为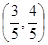 ,求
,求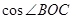 的值;
的值;
(2)若 ,四边形
,四边形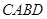 的周长为
的周长为 ,试将
,试将 表示成
表示成 的函数,并求出
的函数,并求出 的最大值.
的最大值.
已知在等比数列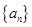 中,
中,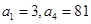 ,若数列
,若数列 满足:
满足: ,数列
,数列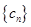 满足:
满足: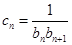 ,且数列
,且数列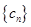 的前
的前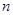 项和为
项和为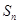 .
.
(1)求数列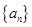 的通项公式;(2)求数列
的通项公式;(2)求数列 的通项公式; (3) 求
的通项公式; (3) 求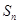 .
.