(本小题满分12分)
设数列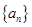 满足
满足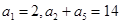 ,且对任意
,且对任意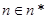 ,函数
,函数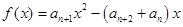 满足
满足 .
.
(1)求数列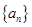 的通项公式;
的通项公式;
(2)设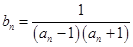 ,记数列
,记数列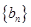 的前项和为
的前项和为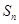 ,求证:
,求证: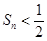 .
.
已知函数f(x)=x+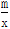 ,且f(1)=3.
,且f(1)=3.
(1)求m;
(2)判断函数f(x)的奇偶性.
已知全集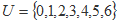 ,集合
,集合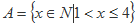 ,
,
(1)用列举法表示集合A与B;
(2)求 及
及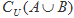
(本小题满分12分)设O为坐标原点,曲线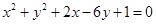 上有两点P,Q关于直线
上有两点P,Q关于直线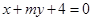 对称.
对称.
(1)求实数m的值;
(2)是否存在直线PQ,满足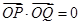 ,若存在求出直线方程;若不存在,说明理由.
,若存在求出直线方程;若不存在,说明理由.
(本小题满分12分)某高级中学共有学生2 000名,各年级男、女生人数如下表:
| 高一年级 |
高二年级 |
高三年级 |
|
| 女生 |
373 |
X |
Y |
| 男生 |
377 |
370 |
Z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知y≥245,z≥245,求高三年级中女生比男生多的概率.
(本小题满分12分)已知圆C: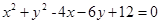 ,点A(3,5)求:
,点A(3,5)求:
(1)过点A的圆的切线方程;
(2)O是坐标原点,连接OA,OC,求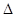 AOC的面积S.
AOC的面积S.